Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Интегрирование дробно-рациональных функций

Дробно-рациональной функцией или рациональной дробью называется отношение двух многочленов

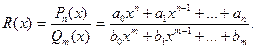
Если 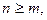то рациональная дробь называется неправильной, при n< m, дробь называется правильной. Всякую неправильную рациональную дробь можно представить (делением числителя на знаменатель “уголком”) в виде суммы многочлена и некоторой правильной дроби

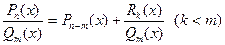
Интегрирование дробно-рациональной функции сводится к интегрированию многочлена и правильной рациональной дроби. Так как интегрирование многочленов не представляет затруднений, то основная трудность при интегрировании рациональных дробей заключается в интегрировании правильных дробей. Среди правильных рациональных дробей выделяют четыре типа простейших дробей.

1. 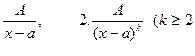, целое). 3.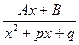

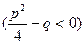
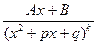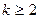(, целое, 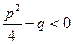).приравнивая числители получившихся дробей, приходим к равенству двух многочленов

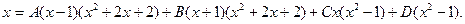
Два многочлена тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях х. Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений для определения A, B, C, D, E.:

при ;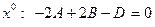

при ;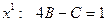

при ;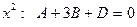

при .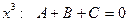

Решив эту систему, найдем коффициенты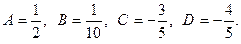

Разложение рассматриваемой дроби имеет вид:

.

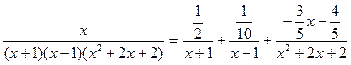Интегрирование простейших дробей.

1. .

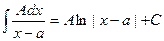2. .

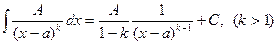3.

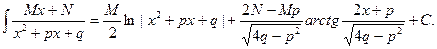
4.

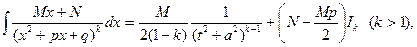
где

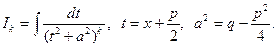
Пример. Найти неопределенный интеграл

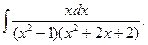
Решение. Используя предыдущее разложение, будем иметь
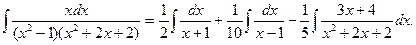
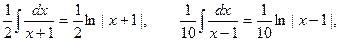
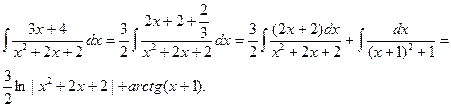
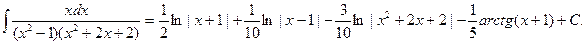