
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Формула Ньютона – Лейбница
|
|
Если функция f(x) непрерывнана сегменте [ a, b ] и функция 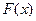 есть некоторая ее первообразная на этом сегменте, то для вычисления определенного интеграла имеет место формула Ньютона-Лейбница.
есть некоторая ее первообразная на этом сегменте, то для вычисления определенного интеграла имеет место формула Ньютона-Лейбница.
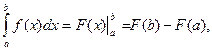
Примеры. Вычислить интегралы.
1. 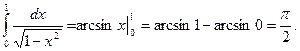
2. 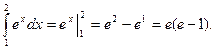
3. 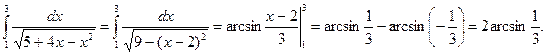
Замена переменной в определенном интеграле
Если функция f(x) непрерывна на сегменте 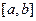 и функция
и функция 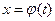 непрерывна вместе со своей производной
непрерывна вместе со своей производной 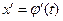 на сегменте
на сегменте 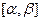 , причем
, причем 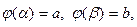 то
то
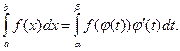
Пример. Вычислить интеграл 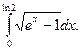
Решение.
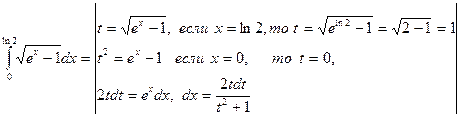 =
= 
= 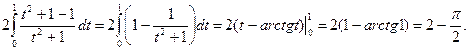
Интегрирование по частям в определенном интеграле
Если функции u(x) и v(x) непрерывны вместе со своими производными u’(x) и v’(x) на сегменте 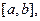 то имеет место формула интегрирования по частям.
то имеет место формула интегрирования по частям.
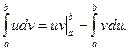
Упражнения
1. 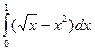 2.
2. 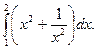
3. 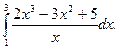 4.
4. 
5. 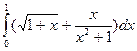 . 6.
. 6. 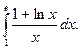
7. 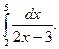 8.
8. 
9.  . 10.
. 10. 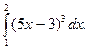
11. 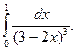 12.
12. 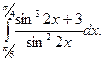
13. 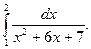 14.
14. 
14. 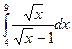 15.
15. 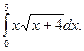
16. 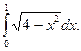 17.
17. 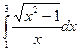
18. 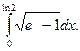 19.
19. 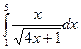
20. 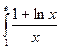 21.
21. 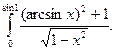
22. 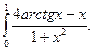 23.
23. 
24. 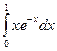 25.
25. 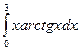
26. 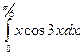 27.
27. 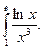
28. 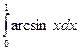 29.
29. 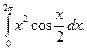
30. 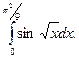 31.
31. 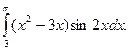
32. 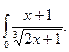 33.
33. 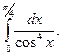
34. 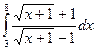 . 35.
. 35. 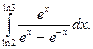
36. 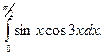 . 37.
. 37. 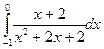 .
.
38. 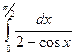 . 39.
. 39. 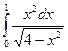 .
.
40. 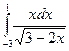 . 41.
. 41. 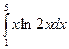 .
.
42. 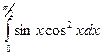 . 43.
. 43. 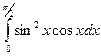 .
.
44. 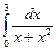 . 45.
. 45. 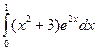 .
.
46. 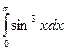 . 47.
. 47. 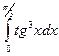 .
.
НЕДЕЛЯ 12
Лекция 23-24
|
|
