Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Приложения определенного интеграла.

В декартовой системе координат за основную фигуру, площадь которой выражается определенным интегралом, принимается криволинейная трапеция. Если y=f(x) – уравнение линии, ограничивающей трапецию, то площадь трапеции S (в предположении, что y³ 0) равна S= 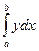, где пределы интегрирования a и b(a< b) - абсциссы начала и конца линии.

Если линия задана параметрическими уравнениями x=j(t), y=y(t), то совершая подстановку в интеграле по формуле x=j(t), получим

S= 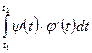, где t₁ и t₂- значения, между которыми изменяется параметр t, когда точка пробегает слева направо всю линию, ограничивающую трапецию сверху.

Пример. Найти площадь S фигуры, ограниченной эллипсом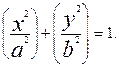

Имеем S=2 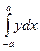, y³ 0. Удобно перейти к параметрическому виду: x=a cos t, y=b sin t. Тогда

S= -2 ab 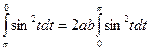=2 ab× 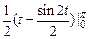= p ab.

Если линия, ограничивающая фигуру, задана уравнением в полярной системе координат, то в качестве основной фигуры принимается криволинейный сектор - фигура, ограниченная линией r=f(j), с которой любой луч, исходящий из полюса P, пересекается не более, чем в одной точке, и двумя лучами j=a и j=b:

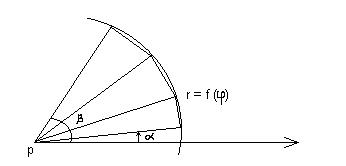
В результате вывода получается формула для вычисления площади фигуры, заключенной между лучами j=a и j=b:

S= .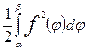

Пусть дано тело, ограниченное замкнутой поверхностью, пусть известна площадь любого его сечения, проведенного плоскостью, перпендикулярной к некоторой прямой, например к оси абсцисс:

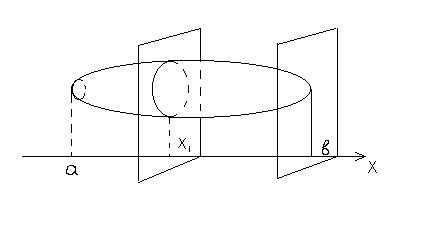
При этом можно считать, что площадь такого сечения является известной нам функцией S(x), где x – абсцисса точки пересечения указанной плоскости с осью х. Далее предполагается, что все тело заключено между двумя перпендикулярными к оси х плоскостями, пересекающими ее в точках a и b (a< b). Для определения объема такого тела разобьем его на слои с помощью секущих плоскостей, перпендикулярных к оси х и пересекающих ее в точках x₀=a, x₂, …, x_n=b. Каждый слой заменим цилиндром с той же высотой и основанием, равным S(x). Объем прямого цилиндра равен произведению площади его основания на высоту. Объем вычисляют как предел при n®¥ суммы объемов, образующих ступенчатое тело и получаем

V=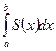

Если тело получено вращением криволинейной трапеции, ограниченной линией y=f(x), вокруг оси Ох, то поперечным сечением с абсциссой х служит круг, радиус которого равен соответствующей ординате линии y=f(x)

S(x)=py² Þ V_x= 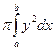, где y=f(x).

Получена формула объема тела, полученного вращением линии y=f(x) вокруг оси Ох. Аналогично получается формула объема тела, полученного вращением трапеции вокруг оси Оу. Там возможны две формулы:

V_y= 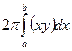или V_y= 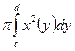, где c и d на оси Оу.

Длина дуги AB кривой y=f(x) есть предел длины вписанной в нее ломаной при неограниченном увеличении числа ее сторон и при стремлении наибольшей из этих сторон к нулю:

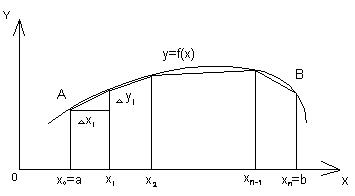
Линия AB задана уравнением y=f(x). Длина дуги AB вычисляется по формуле

L= 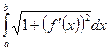или L= .

Если dx внести под знак корня, то формулу можно переписать в виде

L= .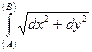

Если уравнение линии задано параметрически: x=x(t), y=y(t) и t_1, t₂ – значение параметра t, соответствующие концам дуги, причем t₁< t₂, то

L=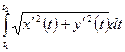

Пусть теперь линия задана уравнением в системе полярных координат: r=r(j). Рассматривая в зависимостях x=rcosj, y=rsinj полярный угол j в качестве параметра, получим

dx=(r¢ cosj-rsinj)dj, dy=(r¢ sinj+rcosj)dj, что дает 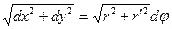и, значит,

L= 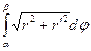, a< b,

где a и b - значения полярного угла соответственно начала А и конца В дуги.

Тело получено вращением вокруг оси Ох криволинейной трапеции, ограниченной сверху линией y=f(x), прямыми x=a и y=b, осью Ох. Площадь поверхности вращения для данного тела определяется по формуле

Q=2 или Q=2 ,

где 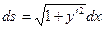- дифференциал длины дуги.