Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 1) Является ли ортогональным линейный оператор , действующий на векторы ортонормированного базиса по формулам
|
|
1) Является ли ортогональным линейный оператор 
, действующий на векторы ортонормированного базиса по формулам
а) 
;
б) 
;
в)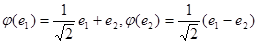 
;
г)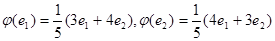 
;
д)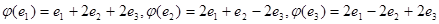 
;
е)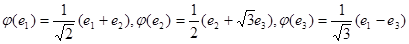 
.
2) Докажите, что если два вектора евклидова пространства имеют одну длину, то существует ортогональный линейный оператор, переводящий один вектор в другой.
3) Пусть даны две системы векторов x 1, …, xk и y 1, …, yk евклидова пространства. Для того, чтобы существовал ортогональный линейный оператор , для которого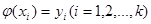 
, необходимо и достаточно, чтобы матрицы Грамма обеих систем векторов совпадали: 
.
4) Докажите, что ортогональное дополнение к линейному подпространству, инвариантному относительного ортогонального линейного оператора, также инвариантно относительно этого оператора.
5) Докажите эквивалентность следующих утверждений
а) линейный оператор ортогонален;
б)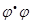 
– тождественное отображение;
в) линейный оператор невырожденный и обратный линейный оператор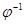 
совпадает с ;
г) линейный оператор 
ортогонален;
д)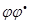 
– тождественное отображение.
6) Найдите ортонормированный базис собственных векторов и матрицу в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей А
а) б)
;.
7) Образуют ли подгруппу в группе всех ортогональных операторов евклидова пространства
а) подмножество операторов с определителем 1;
б) подмножество операторов с определителем -1?
|
|