Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Доказательство. Умножая обе части матричного равенства на матрицу ХТ слева, в правой части получим f

АХ = .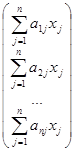

Умножая обе части матричного равенства на матрицу Х^Т слева, в правой части получим f. ■

Формулы 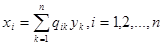называются линейным преобразованием неизвестных с матрицей 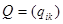. Обозначая через Х столбец из неизвестных 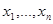, а через Y – столбец из неизвестных 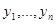, запишем линейное преобразование в виде матричного равенства

X = QY.

Последовательное выполнение линейных преобразований с матрицами Q и R есть линейное преобразование неизвестных с матрицей QR, Если матрица линейного преобразования неизвестных невырожденная, то линейное преобразование называется невырожденным. Для невырожденной матрицы существует обратная, поэтому невырожденное линейное преобразование обратимо: Y = Q^-1X.

Так как произведение невырожденных матриц – невырожденная матрица, то последовательное выполнение невырожденных линейных преобразований есть невырожденное линейное преобразование.

Теорема. Если квадратичную форму 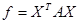подвергнуть линейномупреобразованию X = QY с матрицей Q, то матрица преобразованной квадратичной формы равна Q^TAQ.

Доказательство. = . ■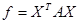

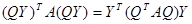Следствие. Знак определителя матрицы квадратичной формы при невырожденном линейном преобразовании не меняется.

Доказательство. В равенстве det Q^TAQ =det A det ² Q по условию det ² Q 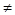0, а поэтому число положительное. Следовательно, числа det Q^TAQ и det A одного знака.