
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства сопряжения
|
|
1) 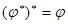 ;
;
2) 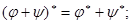
3) 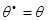 ;
; 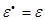 ;
;
4) 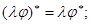
5) 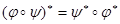 ;
;
6) если линейный оператор невырожден, то 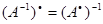 ;
;
7) 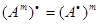 для любого целого неотрицательного m.
для любого целого неотрицательного m.
В силу свойства один линейные операторы  и
и 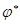 сопряжены друг другу. Свойство 3 в комплексном евклидовом пространстве приобретает вид
сопряжены друг другу. Свойство 3 в комплексном евклидовом пространстве приобретает вид  .
.
Теорема. Если А – матрица линейного оператора  в некотором ортонормированном базисе, то
в некотором ортонормированном базисе, то 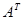 – матрица линейного оператора
– матрица линейного оператора 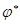 в этом же базисе.
в этом же базисе.
Доказательство. Пусть 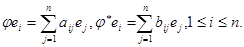 Тогда
Тогда 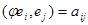 . С другой стороны
. С другой стороны 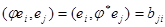 . Отсюда, aij = bji для всех i, j;
. Отсюда, aij = bji для всех i, j;
1  i, j
i, j  n. ■
n. ■
Если  =
= 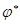 , то линейный оператор
, то линейный оператор  называется самосопряженным.
называется самосопряженным.
Теорема. Матрица самосопряженного линейного оператора в ортонормированном базисе симметрична.
Доказательство.  =
= 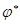
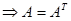 . ■
. ■
Теорема. Если матрица линейного оператора в некотором ортонормированном базисе симметрична, то линейный оператор самосопряженный.
Доказательство. Дано:
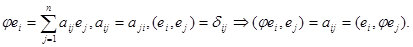
На базисных векторах линейный оператор ведет себя как самосопряженный. Пусть 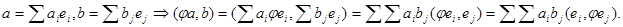
С другой стороны 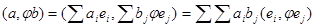 . Правые части равны, поэтому равны и левые части, следовательно, (
. Правые части равны, поэтому равны и левые части, следовательно, (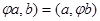 для любых векторов а и b из Е. Это означает, что
для любых векторов а и b из Е. Это означает, что  – самосопряженный линейный оператор. ■
– самосопряженный линейный оператор. ■
Теорема. Собственные векторы самосопряженного линейного оператора, принадлежащие различным собственным значениям, ортогональны.
Доказательство. Пусть 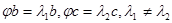 . Тогда
. Тогда
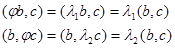
Правые части этих равенств равны, так как линейный оператор  самосопряжен, поэтому равны и левые, т.е.
самосопряжен, поэтому равны и левые, т.е. 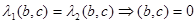 ввиду того, что
ввиду того, что 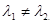 ■
■
Теорема. Корни характеристического многочлена симметрической матрицы с действительными коэффициентами действительны.
Доказательство. Пусть 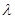 – корень характеристического многочлена матрицы А с действительными коэффициентами. Тогда существует ненулевое решение
– корень характеристического многочлена матрицы А с действительными коэффициентами. Тогда существует ненулевое решение 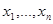 однородной системы линейных уравнений с матрицей
однородной системы линейных уравнений с матрицей  , т.е. имеем систему равенств
, т.е. имеем систему равенств
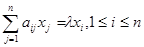 ,
,
где 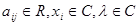 . После умножения каждого из этих равенств соответственно на
. После умножения каждого из этих равенств соответственно на  получим
получим 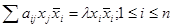 или после суммирования всех равенств
или после суммирования всех равенств 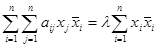 . В этом равенстве перейдем к сопряженным величинам
. В этом равенстве перейдем к сопряженным величинам 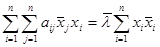 . В силу симметричности матрицы А левые части двух последних равенств равны, поэтому равны и правые части, поэтому
. В силу симметричности матрицы А левые части двух последних равенств равны, поэтому равны и правые части, поэтому 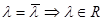 . ■
. ■
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Теорема. Для любой симметрической матрицы A с действительными элементами найдется ортогональная матрица Q, для которой матрица Q -1 AQ диагональная.
Доказательство проведем методом полной математической индукции по порядку n матрицы А. Матрицу А рассматриваем как матрицу линейного оператора  в некотором ортонормированном базисе n- мерного евклидового пространств. Пусть с 1 – собственный вектор линейного оператора
в некотором ортонормированном базисе n- мерного евклидового пространств. Пусть с 1 – собственный вектор линейного оператора  , принадлежащий собственному значению
, принадлежащий собственному значению 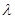 . Он существует, так как все характеристические корни матрицы А действительны. Считаем, что вектор с 1 нормирован и включим его в ортонормированный базис с 1, с 2, …, сn евклидова пространства. Подпространство, натянутое на векторы с 2, …, сn, инвариантно относительно
. Он существует, так как все характеристические корни матрицы А действительны. Считаем, что вектор с 1 нормирован и включим его в ортонормированный базис с 1, с 2, …, сn евклидова пространства. Подпространство, натянутое на векторы с 2, …, сn, инвариантно относительно  и по гипотезе индукции в нем существует базис, в котором матрица линейного оператора, индуцированного линейным оператором
и по гипотезе индукции в нем существует базис, в котором матрица линейного оператора, индуцированного линейным оператором  , диагональна. Тогда матрица линейного оператора
, диагональна. Тогда матрица линейного оператора  в базисе с 1, с 2, …, сn диагональна. Матрица Q перехода от первоначального базиса к базису с 1, с 2, …, сn искомая. ■
в базисе с 1, с 2, …, сn диагональна. Матрица Q перехода от первоначального базиса к базису с 1, с 2, …, сn искомая. ■
|
|
