
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнения. 1) Докажите, что ортогональные матрицы одного порядка образуют мультипликативную группу.
|
|
1) Докажите, что ортогональные матрицы одного порядка образуют мультипликативную группу.
2) Пусть А – комплексная 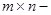 матрица. Матрица
матрица. Матрица 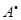 строения
строения 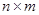 называется сопряженной по отношению к матрице А, если для всех i, j
называется сопряженной по отношению к матрице А, если для всех i, j 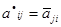 . Докажите свойства:
. Докажите свойства:
а) 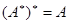 ;
;
б) 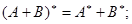
в) 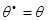 ;
; 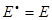 ;
;
г) 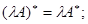
д) 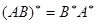 ;
;
е) если линейный оператор невырожден, то 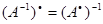 ;
;
ё) 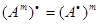 для любого целого неотрицательного m.
для любого целого неотрицательного m.
ж) 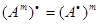 для любого целого m, если матрица А невырожденная;
для любого целого m, если матрица А невырожденная;
з) если f(t) = 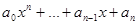 – произвольный многочлен, то
– произвольный многочлен, то 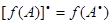 , где
, где 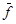 (х) =
(х) = 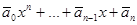 .
.
3) Матрица А называется нормальной, если 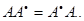 Докажите, что в нормальной матрице скалярное произведение строк i и j равно скалярному произведению столбцов i и j.
Докажите, что в нормальной матрице скалярное произведение строк i и j равно скалярному произведению столбцов i и j.
4) Докажите, что в ортонормированном базисе унитарного пространства матрица нормального оператора нормальна. Обратно, нормальная матрица задает в ортонормированном базисе нормальный оператор.
5) Проверьте, что матрицы нормальные и для каждой найдите ортонормированный базис из собственных векторов
а) 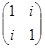 ; б)
; б) 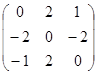 ; в)
; в) 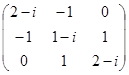 ; г)
; г) 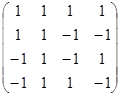 .
.
6) Матрица U называется унитарной, если 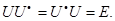 Докажите, что матрица унитарна тогда и только тогда, когда все ее собственные значения по модулю равны единице.
Докажите, что матрица унитарна тогда и только тогда, когда все ее собственные значения по модулю равны единице.
7) Докажите, что унитарные матрицы одного порядка образуют мультипликативную группу.
|
|
