Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Упражнения. 1) Докажите, что линейный оператор невырожденный тогда и только тогда, когда не имеет собственного значения нуль.

1) Докажите, что линейный оператор невырожденный тогда и только тогда, когда не имеет собственного значения нуль.

2) Докажите, что если – невырожденный линейный оператор, то и 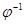имеют одни и те же собственные векторы.

3) Пусть 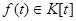и 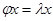, 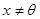. Докажите, что х – собственный вектор и линейного оператора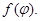

4) Оператор называется нильпотентным, если в некоторой степени равен нулевому. Докажите, что нильпотентный линейный оператор не имеет отличных от нуля собственных значений.

5) Найдите собственные векторы линейного оператора дифференцирования на пространстве, натянутом на cos t и sin t.

6) Докажите, что множество всех собственных векторов линейного оператора , принадлежащих одному и тому же собственному значению, если его пополнить нулевым вектором, является подпространством линейного пространства. Оно называется собственным подпространством линейного оператора , соответствующим этому собственному значению.

7) Докажите, что сумма собственных подпространств прямая.

8) Докажите, что матрица линейного оператора в базисе диагональная тогда и только тогда, когда все векторы базиса являются собственными векторами этого линейного оператора.

9) Докажите, что если все собственные значения линейного оператора различны и принадлежат полю K, то существует базис, в котором матрица этого линейного оператора диагональная.

10) Докажите, что 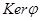и 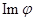– инвариантные подпространства.

11) Найдите собственные векторы линейного оператора, заданного матрицей:

А = .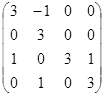

Ответ. Собственные векторы, принадлежащие собственному значению 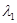= = = = 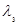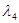3, образуют двумерное пространство с базисом (1, 0, 0, -1) и (0, 0, 1, 0) (выбор базиса неоднозначен).