Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Ортогональный линейный оператор

Если 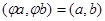, то будем говорить, что линейный оператор сохраняет скалярное произведение векторов а и b, а если 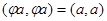, то будем говорить, что линейный оператор сохраняет скалярный квадрат вектора а. Линейный оператор называется ортогональным, если сохраняет скалярный квадрат любого вектора из евклидова пространства.

Теорема. Линейный оператор ортогонален тогда и только тогда, когда сохраняет скалярное произведение для любой пары векторов евклидова пространства.

Доказательство. Дано: 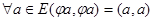. Тогда

.

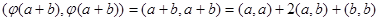С другой стороны,

■

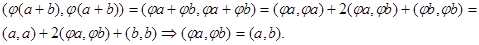Теорема. Матрица ортогонального линейного оператора в ортонормированном базисе ортогональна.

Доказательство. Пусть 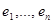– ортонормированный базис Е. Каждый элемент 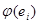можно записать в виде линейной комбинации векторов базиса

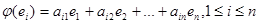
С одной стороны 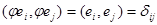в силу того, что линейный оператор ортогональный и базис ортонормированный. С другой стороны, если это же скалярное произведение запишем в координатной форме, то получим 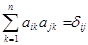, а это означает, что матрица ортогональна. ■

Теорема. Если матрица линейного оператора в некотором ортонормированном базисе ортогональна, то линейный оператор ортогонален.

Доказательство. Дано: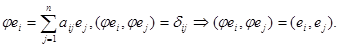

На базисных векторах линейный оператор ведет себя как ортогональный. Следовательно, (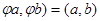 для любых векторов а и b из Е. Это означает, что – ортогональный линейный оператор. ■