Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Упражнения. 1) Линейный оператор А унитарного (комплексного евклидового) пространства называется нормальным, если Докажите

1) Линейный оператор А унитарного (комплексного евклидового) пространства называется нормальным, если 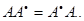Докажите, что линейный оператор нормален тогда и только тогда, когда для него существует ортонормированный базис из собственных векторов.

2) Линейный оператор U унитарного пространства называется унитарным, если 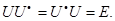Докажите, что нормальный оператор унитарен тогда и только тогда, когда все его собственные значения по модулю равны единице.

3) Линейный оператор Н унитарного пространства называется эрмитовым, если . Линейный оператор K унитарного пространства называется косоэрмитовым, если 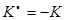. Докажите, что нормальный оператор эрмитов тогда и только тогда, когда все его собственные значения действительны.

4) Эрмитов оператор H унитарного пространства называется неотрицательным, если 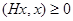для любого ненулевого вектора х. Докажите, что эрмитов оператор неотрицательный тогда и только, когда все собственные значения этого оператора неотрицательны.

5) Эрмитов оператор H унитарного пространства называется положительно определенным, если 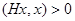для любого ненулевого вектора х. Докажите, что эрмитов оператор положительно определен тогда и только, когда все собственные значения этого оператора положительны.

6) Докажите, что для любого линейного оператора, действующего в унитарном пространстве, существует эрмитово разложение

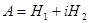, где Н ₁ и Н ₂ – эрмитовы операторы, .

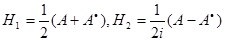7) Докажите, что если А – нормальный оператор, то нормальны также линейные операторы для любой константы 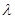, 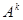для любого натурального k, f(A) для любого многочлена f(t), для невырожденного оператора А, .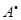

8) Для любого линейного оператора А унитарного пространства существует полярное разложение в виде произведения неотрицательного и унитарного операторов. Докажите это.

9) Докажите, что ядро нормального оператора является ортогональным дополнением к его образу.

10) Докажите, что инвариантное подпространство нормального оператора инвариантно и относительно 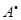.