
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Собственные векторы и собственные значения
|
|
Если существует ненулевой вектор с линейного пространства V/K, для которого 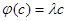 ,
, 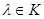 , то
, то 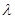 называется собственным значением линейного оператора
называется собственным значением линейного оператора  , а вектор с называется собственным вектором для собственного значения
, а вектор с называется собственным вектором для собственного значения 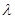 .
.
Теорема. Собственные векторы, принадлежащие различным собственным значениям линейного оператора  , линейно независимы.
, линейно независимы.
Доказательство проведем методом полной математической индукции по числу собственных значений. Пусть 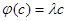 , с
, с 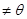 . Один ненулевой вектор образует линейно независимую систему. Предположим, что утверждение верно для любого количества собственных значений < n и пусть
. Один ненулевой вектор образует линейно независимую систему. Предположим, что утверждение верно для любого количества собственных значений < n и пусть 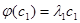 ,
, 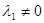 ,
, 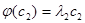 , …,
, …, 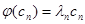 ,
, 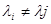 при i
при i 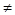 j,
j, 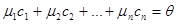 . Подействовав на обе части равенства линейным оператором
. Подействовав на обе части равенства линейным оператором  , получим
, получим
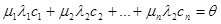 ,
,
а умножив на 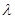 обе части того же равенства
обе части того же равенства
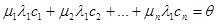 .
.
После вычитания второго из полученных равенств из первого, получим
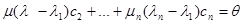 .
.
По гипотезе индукции векторы x 2, ..., xn линейно независимы, поэтому 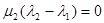 ,...,
,..., 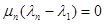
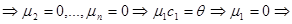 векторы x 1, ..., xn линейно независимы. ■
векторы x 1, ..., xn линейно независимы. ■
Если А – квадратная матрица порядка n, Е – единичная матрица того же порядка, то 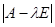 – характеристический многочлен матрицы А. Легко проверить, что характеристические многочлены подобных матриц равны. Поэтому характеристический многочлен матрицы линейного оператора не зависит от выбора базиса и он называется характеристическим многочленом линейного оператора
– характеристический многочлен матрицы А. Легко проверить, что характеристические многочлены подобных матриц равны. Поэтому характеристический многочлен матрицы линейного оператора не зависит от выбора базиса и он называется характеристическим многочленом линейного оператора 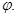
Теорема. Собственными значениями линейного оператора являются корни его характеристического многочлена, лежащие в поле K, и только они.
Доказательство. Пусть 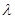 – собственное значение линейного оператора
– собственное значение линейного оператора  . Тогда существует ненулевой вектор с, для которого
. Тогда существует ненулевой вектор с, для которого 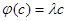 . Пусть А – матрица линейного оператора
. Пусть А – матрица линейного оператора  в некотором базисе e 1, …, en, c =
в некотором базисе e 1, …, en, c = 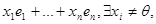
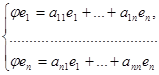
Тогда 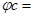
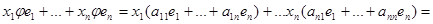


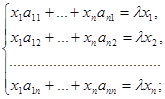

Однородная система n линейных уравнений с n неизвестными x 1, ..., xn имеет ненулевое решение. Поэтому ее определитель равен нулю
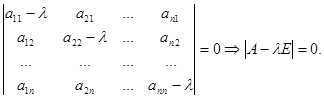
Нетрудно провести все рассуждения в обратном направлении: если 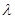 – корень характеристического многочлена, то найдется ненулевой вектор с, для которого
– корень характеристического многочлена, то найдется ненулевой вектор с, для которого 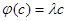 . ■
. ■
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Набор корней характеристического многочлена матрицы линейного оператора называется спектром линейного оператора, причем каждый корень берется с той кратностью, какую он имеет в характеристическом многочлене. Линейный оператор имеет простой спектр, если все его характеристические корни принадлежат основному полю и различны. Для линейного оператора с простым спектром существует базис, в котором матрица линейного оператора диагональная. Подпространство L линейного пространства V/ K называется инвариантным относительно линейного оператора  , если
, если 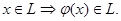 Линейный оператор
Линейный оператор  , рассматриваемый только для векторов инвариантного подпространства L, называется индуцированным на L линейным оператором и обозначается
, рассматриваемый только для векторов инвариантного подпространства L, называется индуцированным на L линейным оператором и обозначается 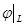 – ограничение
– ограничение  на подпространство L.
на подпространство L.
Пример. Найдите собственные векторы линейного оператора, заданного матрицей
А =  .
.
Составим характеристическую матрицу
А - 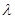 Е =
Е = 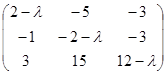 .
.
Так как ее определитель равен 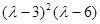 , то корни характеристического уравнения
, то корни характеристического уравнения 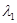 =
=  = 3,
= 3, 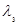 = 6. Для нахождения собственных векторов, принадлежащих собственному значению 3 рассмотрим матричное уравнение (А – 3Е) Х =
= 6. Для нахождения собственных векторов, принадлежащих собственному значению 3 рассмотрим матричное уравнение (А – 3Е) Х = 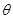 или в координатной форме однородную систему линейных уравнений
или в координатной форме однородную систему линейных уравнений
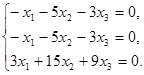
Ранг матрицы системы равен 1, поэтому система равносильна системе из одного уравнения  . Фундаментальная система состоит из двух решений (-5, 1, 0) и (-3, 0, 1). Все собственные векторы, принадлежащие собственному значению
. Фундаментальная система состоит из двух решений (-5, 1, 0) и (-3, 0, 1). Все собственные векторы, принадлежащие собственному значению 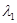 =
=  = 3 записываются в виде
= 3 записываются в виде
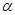 (-5, 1, 0) +
(-5, 1, 0) + 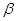 (-3, 0, 1).
(-3, 0, 1).
Для нахождения собственных векторов, принадлежащих собственному значению 6 рассмотрим матричное уравнение (А – 6Е) Х = 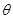 или в координатной форме однородную систему линейных уравнений
или в координатной форме однородную систему линейных уравнений
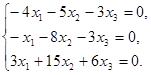
Ранг матрицы системы равен 2, поэтому система равносильна системе из двух уравнений
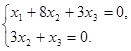
Фундаментальная система состоит из одного решения (- 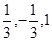 ). Все собственные векторы, принадлежащие собственному значению
). Все собственные векторы, принадлежащие собственному значению 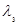 = 6 записываются в виде
= 6 записываются в виде
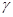 (-
(- 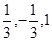 ).
).
Пример. Найдите собственные векторы линейного оператора, заданного матрицей
А = 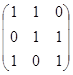
а) над полем вещественных чисел;
б) над полем комплексных чисел.
а) Определитель матрицы (А - 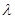 Е) равен -
Е) равен - 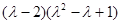 . Характеристическое уравнение над полем вещественных чисел имеет один корень 2. Координаты собственных векторов найдем из системы
. Характеристическое уравнение над полем вещественных чисел имеет один корень 2. Координаты собственных векторов найдем из системы
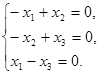
Фундаментальная система решений системы (1, 1, 1). Все собственные векторы, принадлежащие собственному значению 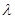 = 2 записываются в виде
= 2 записываются в виде 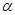 (1, 1, 1).
(1, 1, 1).
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
б) Характеристическое уравнение над комплексных чисел имеет три корня 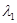 = 2,
= 2, 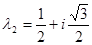 ,
, 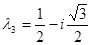 . Все собственные векторы, принадлежащие собственному значению
. Все собственные векторы, принадлежащие собственному значению 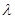 = 2 записываются в виде
= 2 записываются в виде 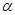 (1, 1, 1).
(1, 1, 1).
Для 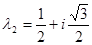 координаты собственных векторов найдем из системы:
координаты собственных векторов найдем из системы:
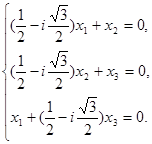
С помощью элементарных преобразований получим эквивалентную систему:
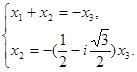
Фундаментальная система решений состоит из одного решения:
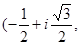
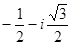 , 1).
, 1).
Таким образом, все собственные векторы, принадлежащие собственному значению 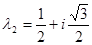 записываются в виде
записываются в виде
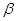
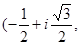
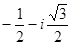 , 1).
, 1).
Аналогично получим, что все собственные векторы, принадлежащие собственному значению 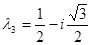 записываются в виде
записываются в виде
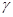
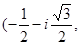
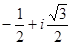 , 1).
, 1).
|
|
