Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Упражнения. 1) Найдите матрицы линейных операторов + и в базисе b1, b2, если матрица в базисе а1 =(-3; 7), а2 = (1; -2) имеет вид

1) Найдите матрицы линейных операторов + 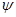и в базисе b ₁, b ₂, если матрица в базисе а ₁ =(-3; 7), а ₂ = (1; -2) имеет вид 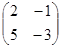, а матрица 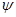в базисе b ₁ = (6; -7), b ₂ = (-5; 6) имеет матрицу .

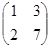2) Докажите, что линейное пространство всех линейных операторов, действующих в одномерном линейном пространстве, одномерно.

3) Линейное пространство 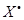всех функционалов, действующих в линейном пространстве Х/K, т.е. линейно отображающих X в K, называется сопряженным с пространством Х. Докажите, что сопряженное линейное пространство 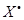изоморфно линейному пространству Х.

4) Говорят, что ненулевой многочлен f(t) = 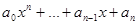аннулирует оператор А, если f(А) = 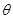. Докажите, что для любого линейного оператора, действующего в n- мерном линейном пространстве, существует аннулирующий многочлен степени .

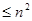5) Пусть m(t) – многочлен наименьшей степени среди всех многочленов, аннулирующих линейный оператор A. Докажите, что m(t) делит любой другой многочлен, аннулирующий линейный оператор A.

6) Докажите, что многочлен m(t) определен линейным оператором А единственным образом с точностью до умножения на постоянный ненулевой множитель. Многочлен m(t) со старшим коэффициентом 1 называется минимальным многочленом линейного оператора А.

7) Линейный оператор А называется нильпотентным, если существует натуральное число q, для которого A^q = 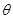. Наименьшее число q, для которого A^q = 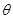, называется индексом нильпотентности линейного оператора А. Докажите, что индекс любого нильпотентного линейного оператора, действующего в n- мерном линейном пространстве, не превосходит n.

8) Найдите минимальный многочлен для оператора проектирования, для оператора отражения, для нильпотентного оператора индекса q.

9) Докажите, что любые два многочлена от одного линейного оператора перестановочны.

10) Докажите, что если линейные операторы А и В перестановочны, то и любые многочлены f(A) и g(A) от этих операторов перестановочны.

11) Докажите, что произведение линейных операторов А и В тогда и только тогда невырождено, когда каждый из операторов А и В невырожден. При этом .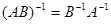

12) Докажите, что для невырожденного линейного оператора А и любой константы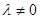

.

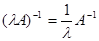13) Докажите, что невырожденные линейные операторы, действующие в линейном пространстве Х/K, являются автоморфизмами, т.е. изоморфизмами Х на себя.

14) Докажите, что невырожденные линейные операторы, действующие в линейном пространстве Х/K, образуют мультипликативную группу.