Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Упражнения. 1) Дифференцирование является линейным оператором линейного пространства всех многочленов от одного переменного с вещественными коэффициентами степени n

1) Дифференцирование является линейным оператором линейного пространства всех многочленов от одного переменного с вещественными коэффициентами степени 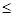n. Найдите матрицу этого линейного оператора в базисе

а) 1, х, х ², …, xⁿ; б) 1, х – с, 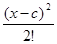, …, 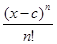; с – вещественное число.

2) Докажите, что следующие условия эквивалентны:

(1) матрица линейного оператора в некотором базисе невырождена;

(2)

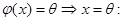
(3) переводит базис в базис;

(4) –инъекция, т.е. ;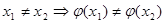

(5) –сюръекция, т.е. ;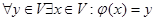

(6) для существует обратный линейный оператор 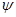, т.е. 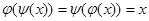для всех х из V.

3) Пусть О ij – правая декартова система координат на плоскости R ². Найдите в этом базисе матрицу линейного оператора поворота R ² на угол 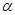вокруг начала координат против часовой стрелки.

4) Пусть i, j, k – правый ортонормированный базис трехмерного евклидова пространства R ³ геометрических векторов. Найдите матрицу линейного оператора Ах = 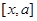, где а – фиксированный вектор с координатами 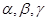в этом базисе.

5) Найдите матрицу оператора дифференцирования в двумерном линейном пространстве, натянутом на базисные функции:

а) 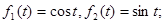б) .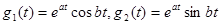

6) Линейное пространство X является прямой суммой подпространств L ₁ и L ₂ , 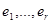- базис подпространства L ₁, 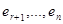– базис L ₂. Найдите в базисе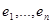

а) матрицу оператора проектирования на L ₁ параллельно L ₂;

б) матрицу оператора проектирования на L ₂ параллельно L ₁;

в) матрицу оператора отражения в L ₁ параллельно L ₂.

7) Линейный оператор А, действующий в трехмерном арифметическом пространстве, переводит линейно независимые векторы 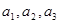в векторы 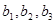, где а ₁ = 5 е ₁ + 3 е ₂ + е _3, а ₂ = е ₁ - 3 е ₂ - 2 е ₃ а ₃ = е ₁ + 2 е ₂ + е ₃;

b ₁ = -2 е ₁ + е _2, b ₂ = - е ₁ + 3 е ₂ , b ₃ =-2 е ₁ - 3 е ₂

Найдите матрицу этого линейного оператора в базисе а) 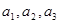; в) .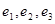

8) В базисе линейного пространства квадратных матриц порядка 2:

.

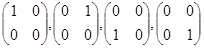записать матрицу линейного оператора

а) транспонирования: Х ;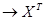

б) G_AB: Х 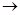АХВ, где А и В – заданные матрицы;

в) F_AB: Х 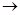АХ + ХВ.

Как изменятся эти матрицы, если в базисе поменять местами матрицы:

?
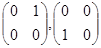