
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Матрица линейного оператора
|
|
Пусть 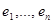 – базис V/K. Каждый элемент
– базис V/K. Каждый элемент 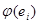 линейного пространства можно записать в виде линейной комбинации векторов базиса
линейного пространства можно записать в виде линейной комбинации векторов базиса
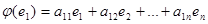
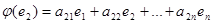 (1)
(1)
… … … … … … …
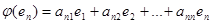
Матрица А с элементами 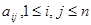 называется матрицей линейного оператора в базисе
называется матрицей линейного оператора в базисе 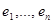 . Соотношения (1) в матричной форме можно переписать так
. Соотношения (1) в матричной форме можно переписать так
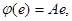 (2)
(2)
где 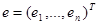 . Рассмотрим квадратные матрицы одного порядка А и В. Матрица В называется подобной матрице А, если существует невырожденная матрица С, для которой В = С-1АС. Обозначается это так:
. Рассмотрим квадратные матрицы одного порядка А и В. Матрица В называется подобной матрице А, если существует невырожденная матрица С, для которой В = С-1АС. Обозначается это так: 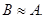
Свойства подобия матриц
1) А  А;
А;
2) А  В
В 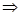 В
В  А;
А;
3) А  В, В
В, В  С
С 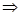 А
А  С:
С:
4) А  В
В 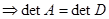
5) А  В
В 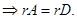
Теорема. Матрицы одного и того же линейного оператора в разных базисах подобны.
Доказательство. Пусть 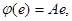
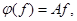 e = Cf, где f и e – базисы линейного пространства, A и B – матрицы линейного оператора
e = Cf, где f и e – базисы линейного пространства, A и B – матрицы линейного оператора  в этих базисах, C – матрица перехода от одного базиса к другому.Тогда
в этих базисах, C – матрица перехода от одного базиса к другому.Тогда
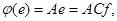
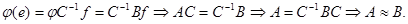 ■
■
|
|
