
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Определение 8.6.
|
|
Критерий  называется байесовским критерием, если для всякого другого критерия
называется байесовским критерием, если для всякого другого критерия  :
:
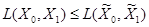 .
.
Указанные способы сравнения критериев не сообщают методов построения «наилучших» критериев – минимаксного, байесовского и рассмотренного ранее наиболее мощного. Заметим, что для построения любого критерия, как было замечено выше, достаточно указать разбиение  выборочного пространства
выборочного пространства  .
.
Выбор разбиения может быть основан на следующем простом рассуждении: пусть получена реализация наблюдения 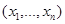 , сравним вероятность получения этой реализации в случае, когда верна гипотеза
, сравним вероятность получения этой реализации в случае, когда верна гипотеза  , и в случае, когда верна гипотеза
, и в случае, когда верна гипотеза  . Если вероятность получения реализации наблюдения
. Если вероятность получения реализации наблюдения 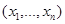 при верной гипотезе
при верной гипотезе  оказывается больше вероятности получения этого же наблюдения при верной гипотезе
оказывается больше вероятности получения этого же наблюдения при верной гипотезе  , тогда предпочтение следует отдать гипотезе
, тогда предпочтение следует отдать гипотезе  , считая, что реализация наблюдения
, считая, что реализация наблюдения 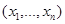 свидетельствует против гипотезы
свидетельствует против гипотезы  . Наоборот, если вероятность получения реализации наблюдения
. Наоборот, если вероятность получения реализации наблюдения 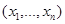 при верной гипотезе
при верной гипотезе  оказывается меньше вероятности получения этого же наблюдения при верной гипотезе
оказывается меньше вероятности получения этого же наблюдения при верной гипотезе  , то предпочтение следует отдать гипотезе
, то предпочтение следует отдать гипотезе  , считая, что реализация наблюдения
, считая, что реализация наблюдения 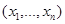 свидетельствует против гипотезы
свидетельствует против гипотезы  .
.
Для придания приведенному рассуждению формального смысла ограничимся рассмотрением только простого случая, удовлетворяющего условиям:
(С1) при  функция распределения
функция распределения  имеет плотность вероятности
имеет плотность вероятности  .
.
(C2) во всем выборочном пространстве  функции плотности
функции плотности 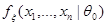 и
и  нигде не равны нулю:
нигде не равны нулю:
 :
:  и
и  .
.
Основная гипотеза  утверждает, что плотность вероятности наблюдения есть функция
утверждает, что плотность вероятности наблюдения есть функция  , а альтернативная гипотеза
, а альтернативная гипотеза  утверждает, что плотность вероятности наблюдения есть функция
утверждает, что плотность вероятности наблюдения есть функция  .
.
Поскольку в силу предположения (С2) плотность вероятности  для всех точек из
для всех точек из  , то во всех точках
, то во всех точках  определено отношение
определено отношение  .
.
|
|
