Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача проверки параметрических гипотез, статистический критерий и функции вероятностей ошибок первого и второго рода. Понятие о равномерно наиболее мощном критерии.

Пусть наблюдение имеет неизвестную функцию распределения , зависящую от параметра , где 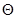– множество допустимых значений параметра .

Пусть 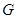– множество функций распределения , получаемых при всевозможных допустимых значениях параметра :

.

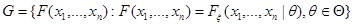Основная гипотеза заключается в том, что неизвестная функция распределения принадлежит некоторому заданному, фиксированному подмножеству :

: .

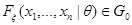Поскольку каждой функции из множества 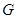соответствуют определенное значение параметра , то множеству функций соответствует подмножество параметров 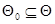такое, что:

.

Отсюда следует, что гипотеза может быть переформулирована в терминах параметра : гипотеза заключается в том, что значение параметра :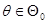

: .

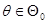Именно поэтому гипотезу принято называть параметрической.

Альтернативная гипотеза в данном случае образована множеством всех функций 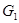, которые не попали в множество :

: ,

.

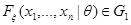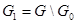В терминах параметра альтернативная гипотеза заключается в том, что:

: ,

.

Предположим, что имеется статистический критерий проверки гипотезы , тогда для каждой реализации наблюдения 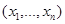критерий либо принимает гипотезу , либо отклоняет гипотезу (принимает гипотезу ). Пусть – выборочное пространство (множество всех возможных реализаций наблюдения):

,

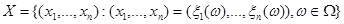тогда в множестве можно выделить подмножество реализаций 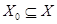, для которых критерий принимает гипотезу , и подмножество реализаций , для которых критерий принимает гипотезу . Фактически задание любого критерия сводится к заданию разбиения множества на множества 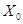и :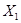

,

,

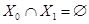поэтому для обозначения критерия далее будем использовать обозначение .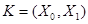

С каждым критерием связаны две ошибки: ошибка первого рода – критерий отклоняет гипотезу в том случае, когда она верна, ошибка второго рода – критерий принимает гипотезу в том случае, когда она не верна (верна альтернативная гипотеза ).