Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение 8.2.

Для критерия 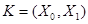вероятностью ошибки второго рода 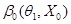называется вероятность:

,

,

где вероятность вычисляется при условии, что функция распределения наблюдения есть функция .

Действительно, если гипотеза не верна, тогда истинное значение параметра , и критерий принимает гипотезу , если наблюдение попадает в множество 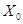, поэтому вероятность ошибки второго рода 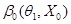есть вероятность того, что наблюдение окажется в множестве 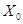, которая вычисляется с функцией распределения при значении параметра . Заметим, что опять же вероятность ошибки второго рода 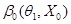зависит от значения параметра и поэтому может оказаться различной при различных значениях параметра.

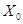Поскольку каждый критерий однозначно определяет разбиение выборочного пространства на подмножества и 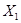, то с каждым критерием однозначно связаны функции ошибок первого и второго родов. Крайне желательно, чтобы вероятности ошибок были как можно меньше, поэтому следует стремиться построить такой критерий, для которого вероятности принимают наименьшее значение.

В общем случае функции вероятностей ошибок первого и второго родов не связаны каким-либо строгим соотношением, поскольку вычисляются при различных функциях распределения и , которые могут быть никак не связаны между собой. Тем не менее, как правило, попытки уменьшения значений вероятностей одной ошибки приводят к увеличению значений вероятностей другой ошибки. Этот эффект возникает из-за того, что функции вероятности ошибок связаны через множества и 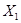. Уменьшение вероятностей ошибок первого рода в большинстве случаев возможно только за счет «сужения» множества 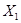, которое приводит к «расширению» множества , и как следствие, совершенно точно не приводит к уменьшению вероятностей ошибок второго рода , а в большинстве случаев приводит к увеличению.

В силу невозможности одновременного уменьшения вероятностей ошибок первого и второго рода иногда поступают следующим образом: изначально задаются некоторым уровнем значимости и рассматривают множество критериев , для которых функция вероятности ошибки первого рода не превосходит значения :

.

Далее сравнивают функции вероятностей ошибок второго рода всех критериев из множества . В общем случае критерии и из множества могут оказаться несравнимыми, поскольку вполне возможно при одних значениях параметра имеет место неравенство , а при других значениях параметра наоборот , тем не менее некоторые критерии все же оказываются сравнимыми.