Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Следствие. В условиях утверждения 8.16 можно показать, что все моменты случайной величины количества шагов до остановки конечны.

В условиях утверждения 8.16 можно показать, что все моменты случайной величины количества шагов до остановки 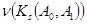конечны.

Среди всех последовательных критериев заданной силы 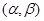ПКОВ 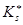силы 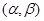имеет наименьшие возможные значения математических ожиданий 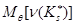(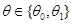). Вычисление величин 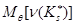в общем случае представляет сложную задачу, тем не менее, в некоторых случаях может быть получено простое приближенное выражение.

Утверждение 8.17. (тождество Вальда)

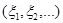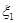Пусть в последовательности случайных величин все случайные величины имеют одинаковое распределение и конечное математическое ожидание , случайная величина принимает значения из множества натуральных чисел, имеет конечное математическое ожидание , и при любом натуральном событие зависит только от случайных величин ,.., . Тогда случайная величина :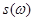

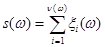
имеет математическое ожидание :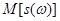

.

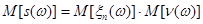Если дополнительно для всех 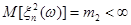, тогда:

.

Теоретическая и практическая задачи регрессионного анализа. Постановка практической задачи линейной регрессии, оценка по методу наименьших квадратов и утверждение о решении нормального уравнения (без доказательства).

Основная задача регрессионного анализа заключается в исследовании зависимости между случайной величиной 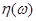и совокупностью случайных величин .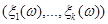