
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Утверждение 8.9.
|
|
Пусть наблюдение 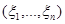 имеет функцию распределения
имеет функцию распределения 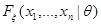 , для которой выполнены условия (С1) и (C2). Если
, для которой выполнены условия (С1) и (C2). Если
1) 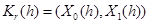 – критерий отношения вероятностей при некотором фиксированном
– критерий отношения вероятностей при некотором фиксированном  такой, что
такой, что 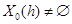 ;
;
2)  – произвольный критерий, отличающийся от
– произвольный критерий, отличающийся от 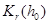 , такой, что
, такой, что 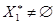 ,
,
Тогда:
 .
.
Заметим, что каждый критерий отношения вероятностей  полностью определяется величиной
полностью определяется величиной  (действительно, по
(действительно, по  однозначно определяется множество
однозначно определяется множество  , и, следовательно, однозначно определяется и множество
, и, следовательно, однозначно определяется и множество  ), поэтому вероятность ошибки первого рода
), поэтому вероятность ошибки первого рода  и вероятность ошибки второго рода
и вероятность ошибки второго рода  для критериев отношения вероятностей являются функциями
для критериев отношения вероятностей являются функциями  :
:
 ,
,
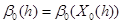 .
.
Понятие о последовательных критериях и применение последовательных критериев в задаче различения двух простых гипотез, вероятности ошибок первого и второго родов и случайная величина количества шагов до остановки.
На каждом шаге последовательный критерий принимает в точности одно из следующих решений:
1. остановиться и принять гипотезу  (отклонить
(отклонить  );
);
2. продолжить и получить следующее наблюдение;
3. остановиться и принять гипотезу  (отклонить
(отклонить  ).
).
Рассмотрим основные положения последовательного анализа на примере следующей простой задачи различения двух простых гипотез. Поскольку количество случайных величин в наблюдении не ограничено, то следует считать, что задана последовательность случайных величин 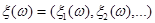 для которой определена последовательность функций распределения
для которой определена последовательность функций распределения  первых
первых  случайных величин:
случайных величин:
 ,
,
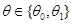 .
.
Основная гипотеза  заключается в том, что
заключается в том, что  , а альтернативная гипотеза
, а альтернативная гипотеза  заключается в том, что
заключается в том, что 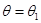 .
.
Для каждого  определим множества
определим множества 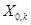 и
и  : пусть
: пусть 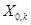 – множество таких последовательностей
– множество таких последовательностей  , для которых критерий
, для которых критерий  выбрал остановку на шаге
выбрал остановку на шаге  и принял гипотезу
и принял гипотезу  , а множество
, а множество  – множество таких последовательностей
– множество таких последовательностей  , для которых критерий
, для которых критерий  выбрал остановку на шаге
выбрал остановку на шаге  и принял гипотезу
и принял гипотезу  .
.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Вполне очевидно, что при фиксированном  :
:
 ,
,
поскольку критерий не может одновременно принять и  и
и  . Кроме того для любых
. Кроме того для любых  и
и  ,
, 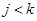 :
:
 ,
,
 ,
,
поскольку критерий не может для одной и той же последовательности  одновременно остановится на шаге
одновременно остановится на шаге  и на шаге
и на шаге  , если остановка произошла на шаге
, если остановка произошла на шаге 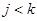 , то шага
, то шага  вовсе не будет.
вовсе не будет.
Каждому последовательному критерию  соответствуют конечные или счетные совокупности множеств
соответствуют конечные или счетные совокупности множеств  и
и  , и наоборот, задание двух совокупностей
, и наоборот, задание двух совокупностей  и
и  однозначно определяет некоторый последовательный критерий
однозначно определяет некоторый последовательный критерий  , поэтому в дальнейшем будем использовать обозначение
, поэтому в дальнейшем будем использовать обозначение 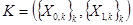 .
.
В соответствии с определением множеств 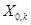 и
и  , множество
, множество  есть множество последовательностей
есть множество последовательностей  , при которых критерий
, при которых критерий  останавливается и принимает гипотезу
останавливается и принимает гипотезу  , множество
, множество  есть множество последовательностей
есть множество последовательностей  , при которых критерий
, при которых критерий  останавливается и принимает гипотезу
останавливается и принимает гипотезу  . Очевидно, что
. Очевидно, что  , но не обязательно
, но не обязательно  .
.
Согласно определению вероятность ошибки первого рода критерия – это вероятность принять гипотезу  в случае, когда верна гипотеза
в случае, когда верна гипотеза  . Последовательный критерий принимает гипотезу
. Последовательный критерий принимает гипотезу  , когда
, когда  , а если верна гипотеза
, а если верна гипотеза  , то
, то 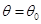 , поэтому вероятность ошибки первого рода критерия
, поэтому вероятность ошибки первого рода критерия  :
:
 ,
,  .
.
где вероятность вычисляется при значении  .
.
Вероятность ошибки второго рода – это вероятность принять гипотезу  в случае, когда верна гипотеза
в случае, когда верна гипотеза  . Последовательный критерий принимает гипотезу
. Последовательный критерий принимает гипотезу  , когда
, когда  , а если верна гипотеза
, а если верна гипотеза  , то
, то 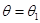 , поэтому вероятность ошибки второго рода критерия
, поэтому вероятность ошибки второго рода критерия 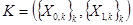 :
:
 ,
,  .
.
|
|
