
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Утверждение 8.14.
|
|
5. Пусть для последовательности случайных величин  функции распределения
функции распределения  первых
первых  величин последовательности удовлетворяют условиям (C1) и (C2). Пусть ПКОВ
величин последовательности удовлетворяют условиям (C1) и (C2). Пусть ПКОВ  с вероятностью 1 останавливается за конечное число шагов, тогда:
с вероятностью 1 останавливается за конечное число шагов, тогда:
6.  ,
,  .
.
Утверждение 8.15.
Пусть для последовательности  случайных величин функции распределения
случайных величин функции распределения  первых
первых  величин последовательности удовлетворяют условиям (C1) и (C2). Пусть заданы числа
величин последовательности удовлетворяют условиям (C1) и (C2). Пусть заданы числа  и
и  ,
,  и
и  , и известно, что ПКОВ
, и известно, что ПКОВ  с вероятностью 1 останавливается за конечное число шагов,
с вероятностью 1 останавливается за конечное число шагов,  и
и  , тогда:
, тогда:
 ,
,
 ,
,
 .
.
Постановка задачи различения двух простых гипотез, «приближенный» критерий отношения вероятностей для заданных вероятностей ошибок, неравенства для вероятностей ошибок «приближенного» критерия отношения вероятностей.
Заметим, что величины  и
и  , как правило, очень малы, поэтому
, как правило, очень малы, поэтому  и
и  , следовательно:
, следовательно:
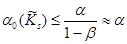 ,
,
 ,
,
поэтому даже если вероятности ошибок ПКОВ  превышают заданные значения
превышают заданные значения  и
и  , то не на много. Уменьшенные вероятностей ошибок ПКОВ
, то не на много. Уменьшенные вероятностей ошибок ПКОВ 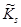 по сравнению с заданными
по сравнению с заданными  и
и  совершенно точно не уменьшают средние количества шагов до остановки, то есть у ПКОВ
совершенно точно не уменьшают средние количества шагов до остановки, то есть у ПКОВ 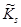 математические ожидания количества шагов до остановки
математические ожидания количества шагов до остановки  скорее всего окажутся больше аналогичных математических ожиданий
скорее всего окажутся больше аналогичных математических ожиданий  ПКОВ
ПКОВ 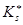 с вероятностями ошибок точно равных
с вероятностями ошибок точно равных  и
и  . Причем разница математических ожиданий, по-видимому, будет тем больше, чем больше различаются вероятности
. Причем разница математических ожиданий, по-видимому, будет тем больше, чем больше различаются вероятности  и
и  , и вероятности
, и вероятности  и
и  .
.
Построение ПКОВ 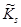 основано на утверждениях 8.14 и 8.15 справедливых для тех ПКОВ, которые с вероятностью 1 останавливаются за конечное число шагов. В общем случае, задача подсчета вероятности остановки произвольного ПКОВ за конечное число шагов может оказаться весьма сложной, поэтому перейдем к рассмотрению более простой задачи, введя дополнительное условие (C3):
основано на утверждениях 8.14 и 8.15 справедливых для тех ПКОВ, которые с вероятностью 1 останавливаются за конечное число шагов. В общем случае, задача подсчета вероятности остановки произвольного ПКОВ за конечное число шагов может оказаться весьма сложной, поэтому перейдем к рассмотрению более простой задачи, введя дополнительное условие (C3):
(C3) Пусть при всех  и
и 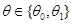 :
:
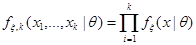 .
.
Другими словами условие (C3) означает, что в последовательности случайных величин 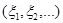 все величины имеют одинаковую плотность вероятности
все величины имеют одинаковую плотность вероятности  и любая конечная совокупность величин является совместно независимой.
и любая конечная совокупность величин является совместно независимой.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
В условиях (С1), (С2) и (С3) отношение правдоподобия на шаге  принимает вид:
принимает вид:
 ,
,
тогда условие продолжения на шаге  ПКОВ
ПКОВ 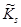 имеет вид:
имеет вид:
 .
.
Поскольку все величины в неравенстве положительные, то вычисляя логарифм от всех частей, получим неравенство:
 .
.
Постановка задачи различения двух простых гипотез и понятие о последовательном критерии отношения вероятностей. Утверждение об остановке последовательного критерия отношения вероятностей и следствие из него. Тождество Вальда и приближенный метод расчета среднего количества шагов до остановки «приближенного» последовательного критерия отношения вероятностей.
Рассмотрим основные положения последовательного анализа на примере следующей простой задачи различения двух простых гипотез. Поскольку количество случайных величин в наблюдении не ограничено, то следует считать, что задана последовательность случайных величин 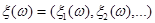 для которой определена последовательность функций распределения
для которой определена последовательность функций распределения  первых
первых  случайных величин:
случайных величин:
 ,
,
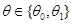 .
.
Основная гипотеза  заключается в том, что
заключается в том, что  , а альтернативная гипотеза
, а альтернативная гипотеза  заключается в том, что
заключается в том, что 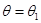 .
.
Для каждого  определим множества
определим множества 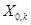 и
и  : пусть
: пусть 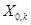 – множество таких последовательностей
– множество таких последовательностей  , для которых критерий
, для которых критерий  выбрал остановку на шаге
выбрал остановку на шаге  и принял гипотезу
и принял гипотезу  , а множество
, а множество  – множество таких последовательностей
– множество таких последовательностей  , для которых критерий
, для которых критерий  выбрал остановку на шаге
выбрал остановку на шаге  и принял гипотезу
и принял гипотезу  .
.
Вполне очевидно, что при фиксированном  :
:
 ,
,
поскольку критерий не может одновременно принять и  и
и  . Кроме того для любых
. Кроме того для любых  и
и  ,
, 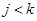 :
:
 ,
,
 ,
,
поскольку критерий не может для одной и той же последовательности  одновременно остановится на шаге
одновременно остановится на шаге  и на шаге
и на шаге  , если остановка произошла на шаге
, если остановка произошла на шаге 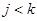 , то шага
, то шага  вовсе не будет.
вовсе не будет.
Каждому последовательному критерию  соответствуют конечные или счетные совокупности множеств
соответствуют конечные или счетные совокупности множеств  и
и  , и наоборот, задание двух совокупностей
, и наоборот, задание двух совокупностей  и
и  однозначно определяет некоторый последовательный критерий
однозначно определяет некоторый последовательный критерий  , поэтому в дальнейшем будем использовать обозначение
, поэтому в дальнейшем будем использовать обозначение 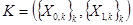 .
.
В соответствии с определением множеств 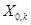 и
и  , множество
, множество  есть множество последовательностей
есть множество последовательностей  , при которых критерий
, при которых критерий  останавливается и принимает гипотезу
останавливается и принимает гипотезу  , множество
, множество  есть множество последовательностей
есть множество последовательностей  , при которых критерий
, при которых критерий  останавливается и принимает гипотезу
останавливается и принимает гипотезу  . Очевидно, что
. Очевидно, что  , но не обязательно
, но не обязательно  .
.
Согласно определению вероятность ошибки первого рода критерия – это вероятность принять гипотезу  в случае, когда верна гипотеза
в случае, когда верна гипотеза  . Последовательный критерий принимает гипотезу
. Последовательный критерий принимает гипотезу  , когда
, когда  , а если верна гипотеза
, а если верна гипотеза  , то
, то 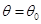 , поэтому вероятность ошибки первого рода критерия
, поэтому вероятность ошибки первого рода критерия  :
:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
 ,
,  .
.
где вероятность вычисляется при значении  .
.
Вероятность ошибки второго рода – это вероятность принять гипотезу  в случае, когда верна гипотеза
в случае, когда верна гипотеза  . Последовательный критерий принимает гипотезу
. Последовательный критерий принимает гипотезу  , когда
, когда  , а если верна гипотеза
, а если верна гипотеза  , то
, то 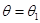 , поэтому вероятность ошибки второго рода критерия
, поэтому вероятность ошибки второго рода критерия 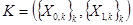 :
:
 ,
,  .
.
|
|
