Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Определение 8.3.

Критерий равномерно мощнее критерия 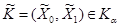, если:

1) : ,

2) : .

Определение 8.4.

Критерий называется равномерно наиболее мощным критерием, если критерий равномерно мощнее любого другого критерия в классе .

В случае если множество состоит из одной точки , то равномерно наиболее мощный критерий иногда называют наиболее мощным критерием (опуская слово равномерно).

В некоторых случаях равномерно наиболее мощного критерия может не существовать.

Постановка задачи различения двух простых гипотез, вероятности ошибок первого и второго рода, понятие минимаксного критерия и байесовского критерия. Понятие критерия отношения вероятностей и теорема о построении минимаксного критерия, байесовского критерия и наиболее мощного критерия как соответствующих критериев отношения вероятностей (без доказательства).

Представим, что множество допустимых значений параметра 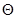состоит всего из двух значений:

.

Отсюда функция распределения либо совпадает с , либо совпадает с . Пусть основная гипотеза заключается в том, что функция распределения 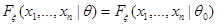или, что тоже самое, :

: ,

: .

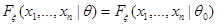Альтернативная гипотеза заключается в том, что или :

: ,

: .

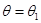Задача проверки гипотезы в указанной постановке называется задачей различения двух простых гипотез.

Легко видеть, что в данном случае множество значений параметра 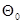, определяемых гипотезой :

,

отсюда,

,

поэтому вероятности ошибок первого и второго рода:

,

,

являются функциями только разбиения 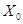и 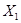. Отсюда следует, что для каждого критерия вероятности ошибок первого и второго рода являются числовыми значениями (а не функциями параметра ), что существенно упрощает способы сравнения критериев.

Критерии можно сравнивать по величинам ошибок: для каждого критерия однозначно определяется наибольшая из двух величин ошибок , поэтому можно считать, что из двух критериев лучше тот, у которого упомянутая наибольшая величина оказывается меньше. Принятый способ сравнения приводит к следующему определению.