
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка задачи проверки простой гипотезы о вероятностях. Применение критерия хи-квадрат к задаче проверке гипотезы о распределении полностью известном.
|
|
Рассмотрим следующую задачу проверки гипотезы: пусть 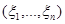 – выборка из неизвестного распределения
– выборка из неизвестного распределения 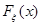 и основная гипотеза
и основная гипотеза  заключается в том, что
заключается в том, что  , где
, где  – известная функция распределения. Требуется предложить критерий проверки гипотезы
– известная функция распределения. Требуется предложить критерий проверки гипотезы  .
.
Воспользоваться критерием хи-квадрат для решения непосредственно поставленной задачи не возможно, тем не менее, имеется возможность сформулировать «близкую» к поставленной задачу, для решения которой использовать критерий хи-квадрат.
Пусть  некоторые числа, рассмотрим разбиение числовой оси на интервалы и полуинтервалы:
некоторые числа, рассмотрим разбиение числовой оси на интервалы и полуинтервалы:
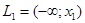 ,
,
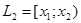 ,
,
…,
 ,
,
 .
.
Зафиксируем некоторый номер  и определим события,
и определим события,
 ,
,
 ,
,
…,
 .
.
Легко видеть, что события 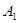 ,
, 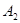 , …,
, …, 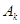 вообще говоря при всех
вообще говоря при всех  одинаковы, поскольку все случайные величины
одинаковы, поскольку все случайные величины  выборки одинаковы (имеют одну и ту же функцию распределения
выборки одинаковы (имеют одну и ту же функцию распределения 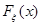 ), и кроме того образуют полную группу событий, поскольку несовместны и их объединение есть множество всех элементарных событий. Определим вероятности
), и кроме того образуют полную группу событий, поскольку несовместны и их объединение есть множество всех элементарных событий. Определим вероятности  ,
, 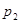 , …,
, …, 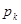 событий
событий 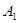 ,
, 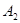 , …,
, …, 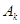 :
:
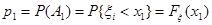 ,
,
 ,
,
…,
 .
.
Рисунок 6.3. Разбиение и вероятности.
Из исходного наблюдения – выборки 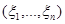 – сформируем вектор
– сформируем вектор  по правилу:
по правилу:
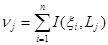 ,
,
 ,
,
то есть  – случайное количество величин выборки
– случайное количество величин выборки 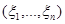 попавших в интервал (полуинтервал)
попавших в интервал (полуинтервал)  .
.
В качестве основной гипотезы рассмотрим «расширенную» гипотезу 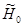 :
:
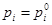 , ,  , ,
 , ,
 ,
…, ,
…,

| (6.7) |
Теперь для проверки «расширенной» гипотезы 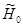 может быть использован критерий хи-квадрат, рассмотренный выше.
может быть использован критерий хи-квадрат, рассмотренный выше.
Из (6.7) следует, что гипотеза 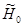 заключается в том, что:
заключается в том, что:
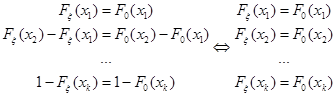
Таким образом, «расширенная» гипотеза 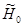 утверждает, что
утверждает, что  только для точек
только для точек 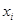 , а гипотеза
, а гипотеза  утверждает, что
утверждает, что  для всех
для всех 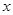 , поэтому
, поэтому  и
и 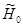 , вообще говоря, различные гипотезы. Фактически,
, вообще говоря, различные гипотезы. Фактически, 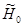 утверждает, что истинное распределение
утверждает, что истинное распределение 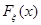 принадлежит некоторому множеству
принадлежит некоторому множеству  :
:
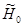 :
:  ,
,
где  – множество таких функций распределения
– множество таких функций распределения  , что
, что 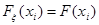 :
:
 .
.
Конечно,  , однако, в
, однако, в  могут оказаться и другие функции
могут оказаться и другие функции  , отличные от
, отличные от  , поэтому гипотеза
, поэтому гипотеза 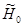 «расширенная».
«расширенная».
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Остается вопрос о выборе точек  , …,
, …, 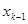 , которые определяют интервалы и события
, которые определяют интервалы и события 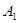 , …,
, …, 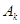 : на практике количество точек выбирают так чтобы,
: на практике количество точек выбирают так чтобы,
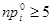 ,
,
при этом местоположение точек выбирают так, чтобы все гипотетические вероятности  оказались приближенно равны между собой:
оказались приближенно равны между собой:
 .
.
Постановка задачи проверки сложной гипотезы о вероятностях и критерий хи-квадрат. Теорема Фишера об асимптотическом распределении минимальной по параметру статистики в случае, если основная гипотеза верна. Замечание об использовании МП-оценок. Применение критерия хи-квадрат к задаче проверки гипотезы о распределении с неизвестным параметром.
Пусть проводится серия из  независимых испытаний, в каждом из которых может произойти в точности одно из событий
независимых испытаний, в каждом из которых может произойти в точности одно из событий 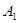 , …,
, …, 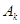 , имеющих неизвестные вероятности
, имеющих неизвестные вероятности  , …,
, …, 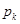 . По результатам серии фиксируются количества наступлений событий
. По результатам серии фиксируются количества наступлений событий 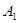 , …,
, …, 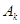 , так что наблюдение представляет собой вектор случайных величин
, так что наблюдение представляет собой вектор случайных величин  , имеющий полиномиальное распределение
, имеющий полиномиальное распределение  .
.
Основная гипотеза  заключается в том, что неизвестные вероятности
заключается в том, что неизвестные вероятности  равны заданным выражениям
равны заданным выражениям 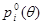 при некотором значении параметра
при некотором значении параметра  (в общем случае параметр
(в общем случае параметр  является
является 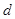 -мерным):
-мерным):
 :
:  , …,
, …,  .
.
Требуется предложить статистический критерий проверки гипотезы  .
.
Заметим, что сформулированная задача, схожа с задачей, рассмотренной в пункте 2, отличие заключается в том, что гипотетические вероятности 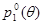 являются не числовыми значениями, а некоторыми функциями параметра
являются не числовыми значениями, а некоторыми функциями параметра  . Указанное отличие не позволяет в качестве статистики критерия использовать статистику
. Указанное отличие не позволяет в качестве статистики критерия использовать статистику  :
:
 ,
,
поскольку статистика 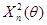 оказывается зависимой от параметра
оказывается зависимой от параметра  , теорема Пирсона (6.15) не может быть применима и как следствие предельное (при
, теорема Пирсона (6.15) не может быть применима и как следствие предельное (при  ) распределение статистики
) распределение статистики 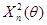 неизвестно. Более того, следует ожидать, что это распределение окажется различным при различных значениях параметра
неизвестно. Более того, следует ожидать, что это распределение окажется различным при различных значениях параметра  . Тем не менее, при специальном выборе параметра
. Тем не менее, при специальном выборе параметра  удается найти предельное распределение.
удается найти предельное распределение.
Предположим, что при каждой реализации наблюдения 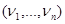 значение параметра
значение параметра  выбирается таким образом, чтобы минимизировать значение статистики
выбирается таким образом, чтобы минимизировать значение статистики  . Минимальные значения статистики
. Минимальные значения статистики  образуют новую статистику
образуют новую статистику  , не зависящую от параметра:
, не зависящую от параметра:
 .
.
Пусть 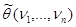 – значение параметра
– значение параметра  , при котором достигается минимальное значение статистики
, при котором достигается минимальное значение статистики  , тогда:
, тогда:
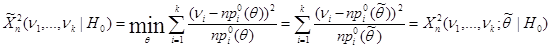
Теорема 6.18. (Фишер)
Пусть наблюдение  имеет полиномиальное распределение
имеет полиномиальное распределение  и основная гипотеза
и основная гипотеза  заключается в том, что:
заключается в том, что:
 :
:  ,
,
где  –
– 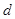 -мерный параметр и
-мерный параметр и 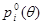 – известные функции. Если гипотеза
– известные функции. Если гипотеза  верна, тогда распределение статистики:
верна, тогда распределение статистики:
— Разгрузит мастера, специалиста или компанию;
— Позволит гибко управлять расписанием и загрузкой;
— Разошлет оповещения о новых услугах или акциях;
— Позволит принять оплату на карту/кошелек/счет;
— Позволит записываться на групповые и персональные посещения;
— Поможет получить от клиента отзывы о визите к вам;
— Включает в себя сервис чаевых.
Для новых пользователей первый месяц бесплатно. Зарегистрироваться в сервисе
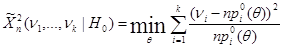 ,
,
стремиться при  к распределению
к распределению 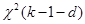 .
.
Без доказательства.
Вычисление статистики  требует трудоемкой операции нахождения минимума, а для решения в общем виде требует нахождения функции
требует трудоемкой операции нахождения минимума, а для решения в общем виде требует нахождения функции 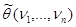 доставляющей минимум статистики
доставляющей минимум статистики  , что существенно затрудняет использование статистического критерия. Оказывается, сформулированная выше теорема Фишера справедлива и в том случае, когда вместо функции
, что существенно затрудняет использование статистического критерия. Оказывается, сформулированная выше теорема Фишера справедлива и в том случае, когда вместо функции 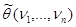 используется МП-оценка
используется МП-оценка  параметра
параметра  , вычисляемая по функции правдоподобия, составленной в соответствии с тем видом функции распределения наблюдения, которую определяет гипотеза
, вычисляемая по функции правдоподобия, составленной в соответствии с тем видом функции распределения наблюдения, которую определяет гипотеза  .
.
Теорема 6.19. (Фишер)
Пусть наблюдение  имеет полиномиальное распределение
имеет полиномиальное распределение  и основная гипотеза
и основная гипотеза  заключается в том, что:
заключается в том, что:
 :
:  ,
,
где  –
– 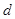 -мерный параметр (
-мерный параметр (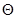 – множество допустимых значений параметра
– множество допустимых значений параметра  ), и функции
), и функции 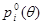 таковы, что:
таковы, что:
1)  (
(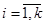 ),
),
2) существуют и непрерывны производные  (
(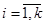 ,
,  ),
),
3) существуют и непрерывны производные  (
(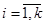 ,
,  ,
,  ),
),
4) для всех  ранг матрицы, образованной частными производными,
ранг матрицы, образованной частными производными,  равен
равен 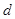 .
.
Если гипотеза  верна и
верна и  – МП-оценка параметра
– МП-оценка параметра  , тогда распределение статистики,
, тогда распределение статистики,
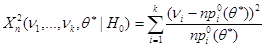
стремится при  к распределению
к распределению 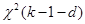 .
.
Без доказательства.
В качестве критической области  выбирается область вида:
выбирается область вида:
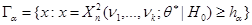 ,
,
где пороговое значение  выбирается исходя из заданного уровня значимости
выбирается исходя из заданного уровня значимости  как квантиль уровня
как квантиль уровня  распределения
распределения  . В остальном статистический критерий аналогичен статистическому критерию хи-квадрат, рассмотренному в пункте 2.
. В остальном статистический критерий аналогичен статистическому критерию хи-квадрат, рассмотренному в пункте 2.
Применение критерия хи-квадрат к задаче проверки гипотезы о распределении с неизвестным параметром.
Пусть  – выборка из неизвестного распределения
– выборка из неизвестного распределения 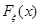 и основная гипотеза
и основная гипотеза  заключается в том, что
заключается в том, что  , где
, где  – функция распределения известная с точностью до значения параметра
– функция распределения известная с точностью до значения параметра  . Требуется предложить критерий проверки гипотезы
. Требуется предложить критерий проверки гипотезы  .
.
На практике сформулированную задачу заменяют другой, но «близкой» задачей: выбираются точки  и рассматривается разбиение числовой оси на полуинтервалы и интервалы:
и рассматривается разбиение числовой оси на полуинтервалы и интервалы:
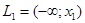 ,
,  , …,
, …, 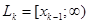 .
.
Рассматриваются события 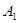 , …,
, …, 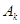 :
:
 .
.
Легко видеть, что,
 ,
,
 ,
,
…,
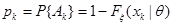 .
.
Для исходной выборки 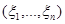 определяется вектор
определяется вектор  так, что:
так, что:
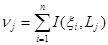 ,
,
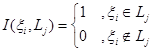 .
.
В качестве основной гипотезы рассматривается «расширенная» гипотеза 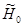 :
:
 ,
, 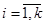 ,
,
 ,
,
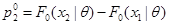 ,
,
…,
 .
.
Для проверки гипотезы 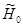 используется статистический критерий со статистикой
используется статистический критерий со статистикой  , где
, где  – МП-оценка параметра
– МП-оценка параметра  .
.
В качестве критической области  выбирается область вида:
выбирается область вида:
 ,
,
где  – квантиль уровня
– квантиль уровня  распределения
распределения 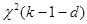 и
и  – заданный уровень значимости.
– заданный уровень значимости.
На практике, как правило, сперва вычисляется МП-оценка  , и лишь затем производится разбиение числовой оси с помощью точек
, и лишь затем производится разбиение числовой оси с помощью точек  , …,
, …, 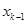 так чтобы
так чтобы  .
.
|
|
