Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Утверждение 6.14.

Пусть наблюдение имеет полиномиальное распределение 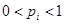, и основная гипотеза заключается в том, что ().

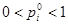Если гипотеза не верна, тогда последовательность (по ) случайных величин не ограничена по вероятности, то есть:

, при .

В силу утверждения 6.14 статистика отвечает условию а) определения статистики критерия 6.5: в случае если гипотеза не верна, статистика с большой вероятностью примет «большое» значение, которое укажет на «большое» расхождение между наблюдаемыми величинами и ожидаемыми значениями.

Для того, чтобы статистика отвечала и пункту б) определения статистики критерия и могла быть использована в статистическом критерии, остается лишь найти способ вычисления (хотя бы приближенного) значений функции распределения статистики . Оказывается, что в случае если гипотеза верна (то есть , ) распределение статистики с ростом стремится к распределению .

Теорема 6.14. (Пирсон)

Пусть наблюдение имеет полиномиальное распределение (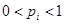). Если верна гипотеза :

: , ,

тогда распределение статистики стремится к распределению хи-квадрат с степенью свободы:

, при .

Можно показать, что критерий хи-квадрат является состоятельным: в данном случае наблюдение имеет полиномиальное распределение , полностью определяемое вектором вероятностей и числом .