Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Определение 6.13.

Критерий называется состоятельным, если мощность критерия при любой альтернативе стремится к 1 при возрастании :

.

На практике не всегда используют наилучшие в смысле функции мощности критерии, поскольку существенную роль может иметь сложность вычисления критерия. В условиях ограниченного времени, когда решение о том принимается гипотеза или отклоняется нужно сделать за короткий промежуток времени, зачастую применяются менее мощные критерии, но более простые в смысле вычисления.

Постановка задачи проверки простой гипотезы о вероятностях и критерий хи-квадрат. Утверждение о неограниченности по вероятности статистики критерия хи-квадрат при условии, что основная гипотеза не верна (без доказательства). Теорема Пирсона об асимптотическом распределение статистики критерия хи-квадрат при условии, что основная гипотеза верна (без доказательства). Состоятельность критерия хи-квадрат. Нецентральное распределение хи-квадрат и асимптотическое распределение статистики критерия хи-квадрат при условии, что основная гипотеза не верна. Условие применимости критерия хи-квадрат на практике.

Представим себе, что проводится серия независимых испытаний, в каждом из которых происходит в точности одно из событий 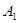, , …, (события образуют полную группу событий), имеющих неизвестные вероятности , , 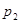…, (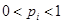). По результатам серии фиксируется количество наступлений события 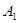, количество наступлений , и так далее до , так что наблюдение представляет собой вектор , имеющий полиномиальное распределение, которое будем обозначать :

.

(Заметим, что отсюда в частности следует, что каждая случайная величина имеет распределение Бернулли, действительно, для получим ():

.

Очевидно, то же самое может быть проделано и для любого , поэтому ).

Основная гипотеза заключается в том, что неизвестные вероятности равны заданным вероятностям ():

: , , …, .

Требуется построить статистический критерий проверки гипотезы .

Для решения сформулированной задачи используется критерий хи-квадрат со статистикой критерия следующего вида:

.

Статистика отражает «суммарное» отклонение наблюдаемых количеств наступлений событий , от ожидаемых средних количеств наступлений событий – , причем каждое отклонение входит в сумму с «весом» , учитывающим величину гипотетической вероятности .

Оказывается, что в том случае, когда гипотеза не верна, статистика с большой вероятностью принимает «большие» значения (утверждение 6.14), поэтому гипотезу следует отклонять, если значение статистики оказалось «большое», то есть в качестве критической области гипотезы следует брать области вида:

,

где – некоторый порог, выбираемый из условия заранее заданного уровня значимости . По определению уровень значимости есть вероятность:

,

,

откуда следует, что в качестве порога следует брать квантиль уровня того распределения статистики , которое определяется гипотезой . Точное выражение для функции распределения найти затруднительно, однако, можно показать (теорема 6.15), что если гипотеза верна, то функция распределения при возрастании стремится к функции распределения хи-квадрат с степенью свободы, то есть при больших :

.

Таким образом, проверка гипотезы сводится к следующей последовательности действий:

1) по заданному уровню значимости определяется квантиль уровня распределения ;

2) по реализации наблюдения (числовым данным, полученным в результате проведения эксперимента) вычисляется значение статистики ;

3) если , тогда гипотеза отклоняется, если , тогда гипотеза принимается.

Перейдем к доказательству основных фактов, использованных при формулировке критерия. Прежде всего, покажем, что в случае, когда гипотеза не верна, значения статистики неограниченно возрастают с ростом .