
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Тема: показникова та логарифмічна функції
|
|
1. Знайти всі цілі значення x, що задовольняють нерівності
.
Розв’язання: область визначення лівої частини нерівності . Значить, нам досить розглянути три значення x: 1, 2, 3.
Якщо , То ліва частина дорівнює
.
Якщо , То
.
Якщо , То
.
Відповідь: 1; 2.
2. Знайти всі цілі x, що задовольняють нерівності
.
Розв’язання: розглянемо функцію .
Доведемо, що, починаючи з деякого x, f (x) зростає. Це можна було зробити звичайним шляхом, оцінюючи похідну. Ми зробимо інакше. Нам достатньо довести зростання функції для цілих x, тобто що .
Маємо
.
Остання нерівність виконується при , Тобто для всіх допустимих цілих x.
Нам залишилося знайти найбільше ціле, для якого (Або найменше, для якого
).
Доведемо, що .
Далі, .
Відповідь: -1, 0, 1, 2 [22].
3. Знайти всі значення параметра , При яких існує єдине значення
, при якому виконується нерівність:
.
Розв’язання: Позначимо (
) і перейдемо до основи 5. Отримаємо:
.
Функція від , розташована в чисельнику, монотонно убуває. Неважко підібрати значення
, При якій вона звертається в нуль:
.
Якщо , то рішенням нерівності щодо
буде
.
А отже, вихідна нерівність не може мати єдиного Розв’язання: (нерівність при будь-якому
має нескінченно багато розв’язань)
Отже, і рішенням щодо
буде
.
Повертаючись до , отримаємо
. Для того щоб існувало єдине значення
, Що задовольняє останнім нерівностей, необхідно і достатньо, щоб найменше значення квадратного тричлена
дорівнювало б 4, тобто
.
Відповідь: [5].
4. При будь-якому значенні параметра a розв’язати нерівність:
.
Розв’язання: розглянемо площину і зобразимо на ній безліч точок, координати яких задовольняють нерівності рис.7.

Рис. 7.
Спочатку зобразимо область, для точок якої має сенс . Це буде пывплощина
(Правіше і нижче прямої
), з якої вилучені частини прямих
.
Після потенціювання нерівності отримаємо . Останньому нерівності відповідає область під параболою
(при цьому
).
Усередині смуги буде
. На малюнку 5 область
, для точок якої
є заштрихованою.
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Тепер вісь точками
розбита на шість ділянок, на кожному з яких легко виписується рішення нашого нерівності. Для цього беремо
на відповідній ділянці, проводимо горизонтальну пряму, знаходимо значення
, на відповідних кінцях відрізків цієї прямої, що потрапили в заштрихованную зону.
Наприклад, якщо , То отримуємо два відрізки, кінці першого:
і
(Менший корінь рівняння
), Другого:
і
.
Відповідь: якщо ,
, розв’язків немає;
якщо , то
;
якщо , то
і
;
якщо , то
і
;
якщо , то
і
;
якщо , то
; якщо
, То
і
[4].
5. Розв’язати рівняння: 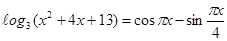
Розв’язання: оцінимо ліву і праву частини рівняння:
а),  так как, х² +4х+13≥ 9, а
так как, х² +4х+13≥ 9, а 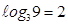
б)  , оскільки
, оскільки  .
.
Оцінка частин рівняння показує, що ліва частина не менше, а права не більш двох при будь-яких допустимих значеннях змінної x. Отже, дане рівняння рівносильне системі:


Перше рівняння системи має тільки один корінь х = -2. Підставляючи це значення в друге рівняння отримуємо вірну числову рівність:

 .
.
Відповідь: 2
6. Розв’язати рівняння: 

Розв’язання: оцінимо ліву і праву частини рівняння:
 ;
; 


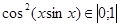
 - сума одиниці і від’ємного числа, тому рівність можлива тільки за умови:
- сума одиниці і від’ємного числа, тому рівність можлива тільки за умови: 
 /
/
Розв’яжемо друге рівняння:  ,
,  ,
,
 , х² +х=0.
, х² +х=0.
Корені: х=0 і х=-1.
Перевіримо справедливість першої рівності, підставивши ці корені. При х = 0, отримуємо правильну рівність, при х = -1 -невірну. Значить, дане рівняння має єдиний корінь х = 0.
Відповідь: х = 0
|
|
