Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно.
Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите; — Персонализирует скидки, чаевые, кешбек и предоплаты; — Увеличивает доходимость и помогает больше зарабатывать;
IV. Практикум.
|
|
За результатами індивідуальної роботи над темою: «Тригонометричні рівняння і нерівності» (пролонгована самостійна робота)клас поділено на шість груп. Кожному групі пропонується шість завдань, з яких виконати потрібно лише три за вибором, чим підтвердити свій рівень або підвищити його.
Порядок виконання практикуму:
Кожне обране завдання виконується на окремому аркуші і зразу після виконання передається на перевірку викладачу. При цьому є економія часу для перевірки. Зараховані бали вносяться до зведеної відомості.
Також учням потрібно виконати обов’язкове завдання.
1. Розв’язати тригонометричне рівняння різними способами.
1-й спосіб. Зведення рівняння до однорідного відносно синуса і
косинуса.
Розкладемо ліву частину за формулами подвійного аргументу, а праву частину замінимо тригонометричною одиницею:
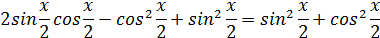
- однорідне рівняння першого степеня.
, оскільки, якщо 
то і 
=0, що суперечить тотожності
, тому ділимо обидві частини рівняння на 
Одержимо 
; або 
2-й спосіб. Розкладання лівої частини рівняння на множники.
Оскільки 
, а 
то 
одержали рівняння, яке розглянули в першому випадку.
3-й спосіб. Перетворення різниці (або суми) тригонометричних функцій в добуток
Запишемо рівняння у вигляді
За формулою різниці двох синусів одержимо
;
; 
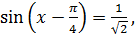
А далі як в попередньому випадку.
4-й спосіб. Зведення до квадратного рівняння відносно однієї з функцій.
, то 
,
; 
Піднесемо обидві частини рівняння до квадрата
Піднесення до квадрата могло призвести до появи сторонніх розв’язків, тому обов’язково необхідна перевірка. Виконаємо її. Одержані розвязки рівносильні об’єднанню трьох розв’язків.
x1 та x2 співпадають з раніше одержаними, тому не є сторонніми.
Перевіримо 
.
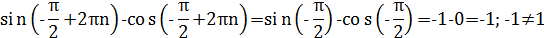
Тоді 
Відповідь: 
5-й спосіб. Піднесення до квадрата обох частин рівняння.
; 
Перевіримо, чи не одержали сторонніх розв’язків
Перевірка показує, що x1 та x4 – сторонні розв’язки.
Відповідь: 
6-й спосіб. Графічне розв’язання.
Запишемо рівняння у вигляді:
Побудуємо графіки функцій:
Абсциси тонок перетину цих графіків будуть розвязками даного рівняння.
Відповідь: 
Диференційовані картки:
 | |||
 | |||
|
|