Тема: геометричні тіла. об’єми та площі поверхонь геометричних тіл. 1. Об’єм піраміди AВСD дорівнює 5

1. Об’єм піраміди AВСD дорівнює 5. Через середини ребер AD і BC проведено площину, що перетинає ребро CD в точці М, при цьому DM: MC = 2: 3. Обчислити площу перерізу піраміди цією площиною, якщо відстань від неї до вершини А дорівнює 1.

Розв’язання. Проведемо пряму через точку М і середину Р ребра ВС, і нехай L - точка перетину прямих PM і BD. Застосовуючи теорему Менелая до трикутника BCD і прямої PL, отримаємо: . Звідси. 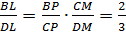. Позначимо за К середину ребра AD, а за Q - точку перетину прямих KL і АВ. Застосовуючи теорему Менелая до трикутника BAD і прямої KL, отримаємо: . Звідси . З’єднавши точку Q з точкою P, а точку K з точкою M, отримаємо шуканий переріз PQKM. Зауважимо, що так як AK = KD, то відстань від Олімпіадні задачі з математики з розв’язками для учнів середньої школи точки D до площини PQKM дорівнює відстані від точки А до цій же площини, тобто дорівнює 1. З’єднаємо тепер точку А з точками Р і М, а точку D з точками P і Q. І зауважимо, що піраміда ABCD складається з пірамід APQKM, DPQKM, APCM і DPQB. Позначивши за S площу перерізу PQKM, отримаємо:

.

Pвідки знаходимо, що S = 3.

2. Ребро правильного тетраедра дорівнює а. Знайдіть найбільше значення площі проекції цього тетраедра на площину.

Розв’язання: нехай ABCD – піраміда, кожне ребро якої дорівнює a (Рис.8). Неважко довести, що протилежні ребра такий піраміди попарно взаємно перпендикулярні. Дійсно, якщо DO - висота піраміди, то O - центр правильного трикутника ABC. AO = пр._{( ABC )} AD, AO ^ BC Þ AD ^ BC (за теоремою про три перпендинуляри).

При проектуванні піраміди ABCD на площину можливі 2 випадки.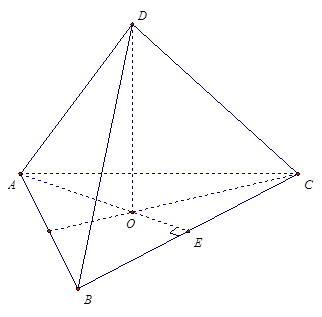

Рис.8

Випадок 1. Трикутник ABC проектується в трикутник A ₁ B ₁ C ₁, а точка D – в точку, яка належить трикутнику A ₁ B ₁ C ₁.

Проекція тетраедра – ∆ A ₁ B ₁ C ₁. S_{∆ A 1 B 1 C 1} ≤ S_{∆ ABC} = .

Випадок 2. Точка D проектується в точку D₁, що належить зовнішньої області трикутника A ₁ B ₁ C ₁. Проекція тетраедра в цьому випадку – читирикутник A ₁ C ₁ D ₁ B ₁ (Рис.9.). = ½ A ₁ D ₁ · C ₁ B ₁ · sin Ð A ₁ OB ₁. максимальна, якщо A ₁ D ₁ = C ₁ B ₁ = a і Ð A ₁ OB ₁ = 90⁰.

Рис. 9.

Така ситуація можлива, якщо площина p паралельна кожній з двох приявих, що перетинаються AD і BC. В цьому випадку: = .

Очевидно, що: .