Формування та розвиток логічного мислення старшокласників засобом нестандартних задач.

Роль математики в розвитку логічного мислення винятково велика тому, що вона є однією із теоретичних наук шкільної освіти. У ній високий рівень абстракції і у ній найбільш природним способом викладу знань є спосіб переходу від абстрактного до конкретного. Це означає, що перед методикою навчання математики постають нові задачі, пов’язані з розвитком логічного мислення. Перші математичні знання засвоюються дитиною у певній, придатній до її розуміння системі, у якій окремі положення логічно пов’язані та випливають одне з одного.

Особливістю логічних умінь є те, що учень повинен не тільки аналізувати, синтезувати, порівнювати, абстрагувати, узагальнювати, але і мислити, робити висновки, встановлювати причинно-наслідкові зв’язки між фактами, процесами, явищами, погоджуючи їх із законами логіки. Тому процес формування логічних умінь передбачає виконання певних послідовних етапів. Це зв’язано як з рівнем загальної підготовки дітей, складністю навчального матеріалу, так і з особливостями мислення дітей відповідної вікової групи.

З метою розвитку логічного мислення учня, вчителю необхідно на кожний урок підбирати пізнавальні завдання. Це дасть можливість сформувати і розвинути всю різноманітність інтелектуальної і творчої діяльності учнів і забезпечити перехід від репродуктивних, формально-логічних дій до творчих.

Основна робота для розвитку логічного мислення повинна здійснюватися одночасно із роботою над задачею. Адже в будь-якій задачі закладені великі можливості для розвитку логічного мислення.

Розв’язування будь-якої задачі - це дуже складаний комплекс дій. Учень повинен мати глибокі математичні знання і вміти використовувати їх в конкретній ситуації, оперувати математичними поняттями володіти сформованими властивостями мислення. Під час розв’язування нестандартних завдань учні оволодівають новими методами та прийомами, засвоюють нові математичні факти, які можуть використовувати під час розв’язання других завдань. Нестандартні задачі корисні ще й тим, що не містять алгоритмічних підходів, потребують проведення аналізу, систематизації, висування гіпотез, стимулюють пізнавальний інтерес учнів, формують навички самостійної роботи, допомагають оволодіти дедуктивним методом.

Нестандартна задача - це завдання, для якої немає в курсі математики загального підходу й алгоритму її розв’язання. Одна і та ж задача може бути нестандартною для одних учнів і стандартною для других, якщо учні володіють прийомами розв’язання такої задачі.

Нестандартні логічні задачі – прекрасний інструмент для такого розвитку. Найбільший ефект при розв’язанні та розумінні задач може бути досягнутий при використанні різних форм роботи над задачею, таких як:

1. Робота над розв’язаною задачею. Багато учнів тільки після повторного аналізу усвідомлюють план рішення задачі. Це шлях до вироблення твердих знань по математиці. Звичайно, повторення аналізу вимагає часу, але воно окупається.

2. Рішення задач різними способами. Мало приділяється уваги рішенню задач різними способами в основному через нестачу часу. Але ж це уміння свідчить про досить високий математичний розвиток.

3. Правильно організований спосіб аналізу задачі - з питання чи від даних до питання.

4. Уявлення ситуації, описаної в задачі (візуалізація). Учитель звертає увагу дітей на деталі, які потрібно обов’язково представити, а якими можна знехтувати. Уявна участь у цій ситуації. Розбивка тексту задачі на значеннєві частини. Моделювання ситуації за допомогою креслення, малюнка.

5. Самостійне складання задач учнями.

Скласти задачу:

- використовуючи слова: більше на, стільки,, менше в, на стільки більше, на стільки менше;

- розв’язувану в 1, 2, 3 дії;

- по даному її плані рішення, діям і відповіді;

6. Рішення задач з відсутніми чи зайвими даними.

7. Зміна питання задачі.

8. Складання різних висловлень за даними задачі і пояснення, що позначає те чи інше вираження. Вибрати ті вираження, що є відповіддю на питання задачі.

9. Пояснення готового рішення задачі.

10. Використання прийому порівняння задач і їхніх розв’язань.

11. Запис двох рішень на дошці - одного вірного й іншого невірних.

12. Зміна умови задачі так, щоб задача зважувалася іншою дією.

13. Яке питання і яка дія зайві в розв’язанні задачі (чи, навпаки, відновити пропущене питання і дія в задачі).

15. Складання аналогічної задачі зі зміненими даними.

16. Рішення обернених задач [3].

Щоб розвивати гнучкість логічного мислення й підтримувати у дітей інтерес до знань, можна на одному занятті давати завдання з різних розділів. Бажано якомога частіше використовувати ігрову форму проведення занять, чергувати індивідуальну роботу дітей з колективною роботою в групах. Доцільно заохочувати дітей самостійно створювати аналогічні завдання та ігри, оскільки це допомагає глибше осмислити матеріал, що опрацьовується.

Для того щоб діти розв’язували нестандартні задачі потрібно:

- по перше, діти повинні мати бажання розв’язувати такі задачі;

- по друге, задачі повинні бути змістовними та цікавими;

- по третє, учні повинні знати деякі методи, що дозволяють почати пошуки розв’язування нестандартних задач [Додаток А].

Схема пошуку розв’язання нестандартної задачі зображена на рис. 4

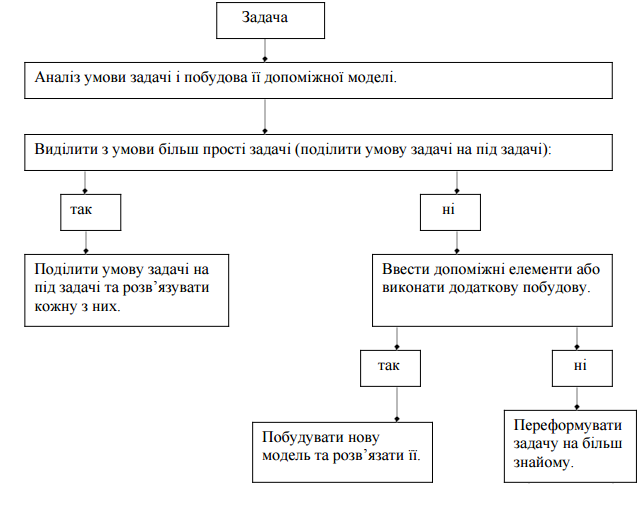
Рис.4.Схема пошуку розв’язання нестандартної задачі.

Наведемо приклади деяких нестандартних задач, які можна використовувати під час вивчення математики в 10 – 11 класах.