Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно.
Чат-бот для мастеров и специалистов, который упрощает ведение записей:
— Сам записывает клиентов и напоминает им о визите
— Персонализирует скидки, чаевые, кешбек и предоплаты
— Увеличивает доходимость и помогает больше зарабатывать
Начать пользоваться сервисом
Начать продвижение сайта
Відповідь: . Тема: геометричні тіла. об’єми та площі поверхонь геометричних тіл
|
|
Тема: геометричні тіла. об’єми та площі поверхонь геометричних тіл
1. Побудуйте переріз куба площиною, що проходить через середину діагоналі і перпендикулярно до неї. Знайдіть площу перерізу, якщо ребро куба дорівнює а.
Розв’язання:
1. B 1 D – діагональ, BD – її проекція на площину основи,
BD ^ AC (властивості діагоналей квадрата). B 1 D ^ AC (за теоремою про три перпендикуляри).
2. Побудуємо площину α, O Î α, B 1 D ^ α. Тоді AC || α.
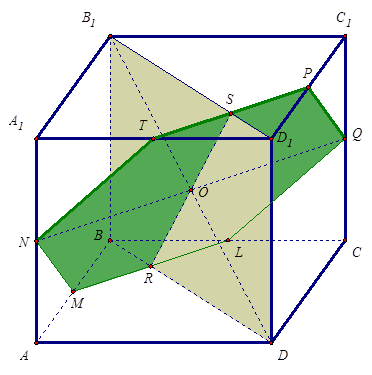
Рис. 8
3. O Î A 1 C 1 CA, O Î NQ, NQ || AC, N Î AA 1, Q Î CC 1, де N – середина AA 1, Q – середина CC 1.
4. D 1 C ^ B 1 D (аналогічно п.1) Þ QP || CD 1, NP || CD 1.
AD 1 ^ B 1 D Þ NT || AD 1, QT || AD 1.
Таким чином, NTPQLM – переріз куба площиною α.
5. Легко показати, що ON = OT = NT = 
. Це означає, що ∆ ONT – правильний, а NTPQLM – правильний шестикутник
Таким чином, Sперерізу = SNTPQLM = 6 SONT =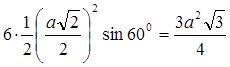 
.
Відповідь: Sперерізу =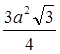 
.
|
|