Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Применение метода ММА к колебательным системам Вопрос 8

Вернёмся к самому простому RLC резонансному контуру (рис. 22). Колебания в нём описываются следующим уравнением

.

Введём безразмерное время t = w ₀ t; после дифференцирования по этой переменной, получим

, где .

(3.22)

Будем решать уравнение в форме (3.15), т. е. через амплитуду и фазу. В этом случае, с учётом (3.16), будет

.

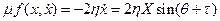Подставляя в укороченные уравнения (3.20) мы получаем

;

.

Эти укороченные уравнения легко интегрируются:

;   .

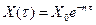Следовательно, колебательный процесс в контуре описывается функцией

,

(3.23)

или в размерном времени

.

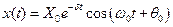(3.24)

Можно, конечно, искать решение уравнения (3.2) методом Лапласа в виде x (t) = X ₀ e^pt, тогда характеристическое уравнение имеет вид

,

корни которого легко найти

,

т. е. общее решение можно записать так

, где .

(3.25)

Сравним теперь решения, полученные разными методами - методом ММА и общим методом Лапласа, т. е. (3.24) и (3.25). Как видно, амплитуда меняется одинаково, а частота определена неправильно: метод ММА говорит, что колебания будут с частотой w ₀, хотя точное решение даёт небольшой сдвиг частоты. Дело в том, что мы сами задаём с самого начала, что колебания будут с частотой w ₀ введением безразмерного времени, т. е. что заложили, то и получили. Мы можем, в принципе, задавать и произвольную частоту w.

Рассмотрим нелинейный контур с конденсатором с сегнетоэлектриком в пренебрежении затуханием (рис. 19). Запишем (2.20) вместе с (2.19):

.

Введём x = q / q ₀, где q ₀ - некоторый заряд, соответствующий ожидаемой максимальной амплитуде колебаний в контуре, тогда наше уравнение примет вид

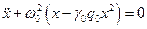, где .

Введём новый масштаб времени t = wt, где w не обязательно совпадает с w ₀. С учётом этой подстановки

.

Вводя обозначение , , получим

.

Учитывая, что мы ограничиваемся случаем | x | < < 1 и g < < 1 (частота колебаний мало отличается от частоты собственных колебаний), можно, отбрасывая член второго порядка малости, приближённо записать

.

Это уравнение принадлежит к типу , и к нему можно применить метод ММА. Используем вариант с медленно меняющимися амплитудами u и v (представление (3.13)), тогда укороченные уравнения, с учётом (3.9), будут иметь вид

;

.

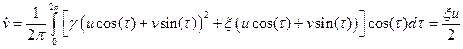Так как нет диссипации, то мы можем сказать, что . Это возможно в случае, если x = 0. Из этого следует, что w = w ₀, т. е. мы теряем неизохронность колебаний (аналогично было в методе последовательных приближений). Таким образом, метод ММА не позволяет найти сдвиг частоты в контуре с квадратичной нелинейностью. Это связано с тем, что метод ММА - метод первого порядка. Чтобы этого избежать, необходимо взять вторые гармоники ряда Фурье.

Рассмотрим колебательный контур с малым нелинейным затуханием, т. е. RLC контур (рис. 22). Рассмотрим колебания с постоянными L и C, но с сопротивлением R (i), зависящим от тока по закону R = R ₀(1 + g ₀ i ²). Это соотношение качественно передаёт зависимость омического сопротивления проводников от протекающего через них тока за счёт их нагрева.

Составим уравнение движения в этом контуре

.

Вводя, как обычно, новые переменные x = q / q ₀ и t = w ₀ t, где , получим уравнение

, где , .

При малом затухании, когда для приближённого решения задачи можно применить метод ММА. Тогда исходное уравнение удобно записать в виде

.

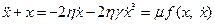Используя (3.15) и (3.16) для X и q имеем укороченные уравнения

;

.

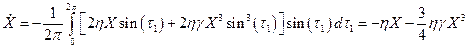Первое из этих уравнений домножим на 2 X и сделаем замену y = X ², тогда

.

После преобразований получаем:

.

Это уравнение легко интегрируется:

, или ,

где D - постоянная, определяемая из начальных условий. Если в начальный момент при t = 0 X (0) = X ₀, то

.

Полученное соотношение для X выражает закон уменьшения амплитуды колебаний в исследуемом нелинейном контуре, начиная от исходного значения X ₀.

Отметим также, что, как следует из проведённого рассмотрения, величиной, определяющей ход процесса, является амплитуда колебаний, а фаза колебаний не играет никакой роли. Это обстоятельство вполне понятно, так как характер движения задаётся исходным запасом колебательной энергии, сообщённой контуру вначале процесса, а фаза колебаний никак не определяет ход колебания - соответствующим выбором произвольного для автономной системы начала отсчёта времени фазу можно сделать любой.