Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Метод ММА для колебательных систем с малыми нелинейностями и потерями при гармоническом силовом воздействии

Общая запись уравнений для неавтономной системы первого порядка при силовом воздействии:

.

(4.18)

В предельном случае если m ® 0, тогда получаем неоднородное ДУ вида

,

решение которого будет x ₀(t) = a cos(w ₁ t), где амплитуда колебаний

.

Возвращаясь к (4.18) и считая нелинейность слабой, будем искать решение в виде

.

(4.19)

Подставляя это решение в исходное уравнение, можно записать

.

Видно, что это уравнение вида (3.8). Для возможности применения метода ММА необходимо потребовать, чтобы внешняя сила была мала по амплитуде и имела бы тот же порядок малости, что и малые силы, связанные с нелинейными и диссипативными свойствами системы и возникающие при конечных амплитудах колебаний в ней. В таком случае воздействующую силу можно объединить с этими малыми силами и свести рассмотрение задачи к приближенному исследованию уравнения типа

,

которое отличается от рассмотренного ранее (см. (3.8)) тем, что функция f ₁ зависит не только от переменной x и её производной, но и явно от времени.

Вводя в исходное уравнение новый масштаб времени t = w ₁ t, получим

.

Вводя обозначение и требуя, чтобы расстройка x была величиной порядка малости m, запишем

.

В правой части этого уравнения малые параметры; обозначив , запишем окончательно

.

(4.20)

Тогда можно решить это уравнение в соответствии с методом ММА.

В качестве простейшего примера рассмотрим вынужденные колебания в контуре с нелинейным затуханием R (i) = R ₀(1 + g ₀ i ²) (см. рис. 26). Для подобного контура мы можем записать уравнение Кирхгофа в виде

.

Если считать, что собственная частота контура w ₀ близка к частоте внешней силы w ₁, то, вводя обозначения

,   ,   ,   ,   ,

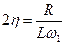приходим к уравнению

,

(4.21)

где

,   .

Для применимости метода ММА к решению этого уравнения необходимо потребовать, чтобы выполнялись неравенства: расстройка x < < 1, затухание в системе 2 h < < 1, амплитуда внешнего воздействия P < < 1, т. е. чтобы все члены в правой части уравнения были малы по сравнению с членами в левой его части.

Решение будем искать в виде (3.15), тогда, вводя t ₁ = t + q, получаем следующие укороченные уравнения

После интегрирования имеем

(4.22)

Стационарные решения находят из укороченных уравнений при условии, что амплитуда и фазовый сдвиг не меняются: , или , , т. е. из системы уравнений

возводя левые и правые части этих уравнений в квадрат и складывая их, получим уравнение

;

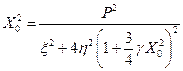оно представляет собой уравнение резонансной кривой для добротного колебательного контура с нелинейным сопротивлением.

При большой нелинейности нельзя предполагать, что решение близко к гармоническому. Мы предполагаем, что есть третья гармоника, т. е. если w ₁ - частота внешнего воздействия, то 3 w ₁» w ₀. Настраиваем контур на эту гармонику и ищем решение (4.20) методом ММА в виде

,

полагая, что

,   .

Результат получается достаточно близким к тому, который даёт метод гармонического баланса.

Полученные выше укороченные уравнения позволяют найти не только стационарные амплитуду и фазу вынужденного колебания, но в принципе и закон установления стационарного процесса путём интегрирования системы укороченных уравнений (4.22). В этом, в частности, заключается большая эффективность метода ММА по сравнению с методом гармонического баланса, дающего в принципе только стационарные значения амплитуд.