
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Генерация высших гармоник Вопрос 11
|
|
Явление, когда появляются высшие гармоники при гармоническом воздействии на нелинейную систему, называется генерацией гармоник.
Рассмотрим, например, колебания в нелинейной консервативной системе с конденсатором с сегнетоэлектриком при достаточно большой амплитуде гармонического воздействия, причём собственная частота малых свободных колебаний системы близка к утроенной частоте воздействия. Для конденсатора с сегнетоэлектриком
 .
.
Уравнение (4.3) будет в этом случае иметь вид:
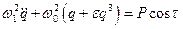 , где , где  . .
| (4.13) |
При большой нелинейности нельзя предполагать, что решение близко к гармоническому. Можно ожидать появления высших гармоник. Мы допустили, что есть третья гармоника, т. е. если w 1 - частота внешнего воздействия, то w 1» w 0/3. В этом случае можно ограничиться только первой и третьей гармониками и искать вынужденные колебания в виде
 ,
,
тогда получается
 .
.
Оставляя в разложении f (q) в ряд Фурье только члены с cos t и cos3 t и приближенно положив - f (q) = a 1cos t + a 3cos3 t, получим систему двух уравнений
 ; ;  . .
| (4.14) |
Для выбранного вида нелинейности имеем

| (4.15) |
Для свободных колебаний системы с нелинейностью (P = 0) из (4.14) получим уравнения
 ; ; 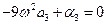 . .
| (4.16) |
Здесь w - основная частота свободных колебаний нелинейной системы, заменившая частоту w 1, которая задавалась внешним воздействием. Из последней системы можно найти соотношение между амплитудами гармоник
 .
.
Нетрудно убедиться, что из системы (4.16) можно получить частоту свободных колебаний:
 .
.
Как мы видим, w отличается от w 0 лишь на величину порядка e.
Иначе обстоит дело при наличии воздействия (P ¹ 0). Тогда частота возбуждаемого колебания будет задаваться внешним воздействием. В рассматриваемом случае частота w 0 близка к 3 w 1. В результате соотношение между амплитудами основного колебания и его третьей гармоники должно быть совсем иным.
Для определения a 1 и a 3 имеем систему (4.14). Заменяя из (4.16) в первом уравнении a 1 на w 2 a 1, получаем
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
 ,
,
откуда выражение для амплитуды основной гармоники
 .
.
Здесь мы учли, что w» w 0 (с точностью до величины порядка e), а w 0» 3 w 1.
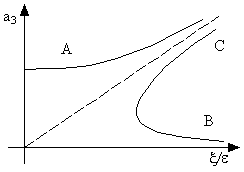 Рис. 31. Амплитуда третьей гармоники.
Рис. 31. Амплитуда третьей гармоники.
| Для определения a 3 воспользуемся вторым соотношением из (4.14), тогда, подставив его во второе уравнение системы (4.15), получим
 .
Введём относительную расстройку x: .
Введём относительную расстройку x:
 ,
тогда получим уравнение третьей степени относительно a 3: ,
тогда получим уравнение третьей степени относительно a 3:
|
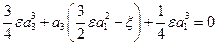 .
.
Так как e ¹ 0, то на e можно сократить
 . .
| (4.17) |
Это решение описывает установившийся процесс. Таким образом, нелинейность зависит от отношения x / e. Зависимость амплитуды третьей гармоники от этого отношения представлена на рис. 31.
|
|
