Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Свободные колебания в резонансном контуре с нелинейной ёмкостью без затухания Вопрос 5

Рассмотрим параллельный резонансный контур, представленный на рис. 19. Здесь в качестве нелинейной ёмкости используется варикап, причём ёмкость разделительного конденсатора Сp много больше ёмкости варикапа Cd. Известен закон изменения ёмкости p-n перехода:	Рис. 19. Колебательный контур с нелинейной ёмкостью.
.	(2.17)
Проинтегрируем (2.17), тогда получим: .

Из последнего уравнения найдём u_ak:

.

(2.18)

В качестве обобщённых координат возьмём напряжение на индуктивности, т. е. u = E + u_ak. Если u = 0, значит к варикапу приложено управляющее напряжение. В этом случае мы можем выразить константы через известные величины. Получается, что q = 0, C_d = C ₀, тогда

.

Подставим эти выражения в (2.18)

,

тогда для обобщённой координаты получаем

, где .

(2.19)

Заметим, что полярность управляющего напряжения E выбрана так, чтобы варикап находился в состоянии обратного смещения, чтобы конденсатор C_р не влиял на работу. Выберем C_p > > C_d, тогда при колебаниях напряжение на C_p не будет сильно меняться и тогда можно считать, что напряжение, приложенное к катушке будет u. В таком случае для контура можно записать второй закон Кирхгофа в виде

Рис. 20. График потенциальной энергии.	.	(2.20)
Уравнение колебаний имеет вид (2.1), что позволяет с учётом (2.19) ввести потенциальную энергию в виде
.	(2.21)
Примерный вид полученной зависимости показан на рис. 20. Перепишем уравнение (2.20) в следующем виде ;   .

Тогда уравнение для фазовой траектории будет выглядеть так:

, где .

(2.22)

Построим фазовый портрет для этой системы методом изоклин. Найдём для этого семейства фазовых траекторий изоклины, т. е. линии с постоянным наклоном. Уравнение изоклин:

,

отсюда, с учётом (2.22), для нашей системы получается

Рис. 21. Построение фазовых траекторий методом изоклин.

. Изоклины, исходя из полученного уравнения, по сути, параболы. Коэффициент ki определяет крутизну. Он может быть как отрицательным, так и положительным, соответственно изоклины будут находиться выше оси или ниже оси абсцисс. Если ki = 0, парабола выльется в вертикальную линию q = 0, а если ki = ¥, то в горизонтальную y = 0. На рис. 21 показано построение фазовых траекторий методом изоклин. Замкнутость фазовых траекторий подтверждает, что мы имеем дело с консервативной системой. Из фазового портрета видно, что при малых амплитудах колебаний, как и в случае идеального маятника, фазовые траектории близки к эллипсам, т. е. малые движения в нелинейной системе близки к гармоническим колебаниям в нелинейной системе. Это связано с тем, что при малых значениях q влиянием нелинейного члена g 0 q 2

по сравнению с линейным членом q на колебательный процесс системе можно пренебречь.

Проделаем то же самое не графически, а аналитически. Воспользуемся методом последовательных приближений. Для этого опять перепишем уравнение (2.20), но уже в форме уравнения (2.10):

.

Опять действуем точно также: установившуюся частоту разложим в ряд

.

Также можно записать, ограничиваясь только первой степенью g ₀,

.

Уравнение нулевого приближения в данном случае имеет вид

;

его решение при начальных условиях будет таким:

.

Первое приближение имеет вид:

.

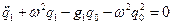Подставляя решение для q ₀, получаем

.

Заметим, на систему с резонансной частотой w воздействует внешняя сила с той же самой частотой, т. е. для секулярных решений получается следующее условие: g ₁ = 0. Таким образом, мы приходим к выводу, что поправка первого порядка отсутствует, поэтому будем раскладывать до следующего параметра, т. е. для частоты, с учётом равенства нулю g ₁, получаем

.

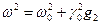Соответственно

.

Тогда уравнение второго приближения, примет вид

.

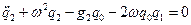Или, подставив решения для q ₀ и q ₁, получим

.

Чтобы исчезли секулярные слагаемые, нужно потребовать, чтобы , тогда мы можем найти зависимость частоты от амплитуды:

.

Итак, мы рассмотрели систему с одной степенью свободы без диссипации. Перейдём теперь к следующему уровню.