Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вынужденные колебания в линейной системе при гармоническом воздействии

Для линейных стационарных систем выполняется принцип суперпозиции: если воздействие x ₁(t) порождает реакцию u ₁(t), а воздействие x ₂(t) реакцию u ₂(t), тогда воздействие, которое является линейной комбинацией первых двух a ₁ x ₁(t) + a ₂ x ₂(t) порождает следующую реакцию a ₁ u ₁(t) + a ₂ u ₂(t). Этот принцип означает, что в таких системах отсутствует нелинейное взаимодействие колебаний, вызванных различными одновременными действующими внешними силами. Будем считать, что собственные колебания в диссипативной системе достаточно быстро затухают, и можно анализировать только вынужденные колебания, т. е. рассматривать установившийся режим

Рассмотрим простейший RLC контур с источником гармонического воздействия u ₁(t) с частотой w ₁ (рис. 26), тогда колебательный процесс будет описываться линейным ДУ:

Рис. 26. Колебательный контур с вынуждающей силой		(4.1)
Решением неоднородного ДУ (4.1) является сумма решений однородного уравнения, т. е. собственных колебаний, и частного решения неоднородного уравнения, т. е. вынужденных колебаний. Собственные колебания описываются уравнением (3.23) , где .

Начальную фазу надо отсчитывать от внешнего воздействия. При гармоническом воздействии внешней силы реакция линейной системы есть гармонический сигнал:

.

Подставим это выражение в (4.1):

.

Воспользовавшись равенством

,

преобразуем получившееся уравнение к виду

.

Приравнивая амплитуды и фазы в правой и левой частях этого уравнения, получим

(4.2)

Мы обозначили g = w ₁/ w ₀ - расстройка, Q ₀ = w ₀ L / R - добротность. Из (4.2) следует, что j ₁(w ₁ ® 0) = 0, j ₁(w ₁ = w ₀) = p /2, j ₁(w ₁ ® ¥) = p.

Решим эту задачу методом комплексных амплитуд. Сопоставим току и напряжению их комплексные амплитуды, а также вспомним реактивные сопротивления, тогда можно записать

.

Найдём модуль

.

Нетрудно видеть, что максимальное значение тока:

.

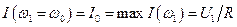Введём форм-фактор, который определяет семейство нормированных резонансных кривых (в данном случае для тока)

.

График этой функции приведён на рис. 27. Напряжение на резисторе пропорционально току через контур u_R = iR, т. е. амплитуда напряжения на резисторе достигает максимума при w ₁ = w ₀. Зависимость фазы напряжения на резисторе от расстройки приведена на рис. 28.

Рис. 27. Семейство нормированных резонансных кривых для разных значений добротности Q 0.

Рис. 28. Зависимость фазы напряжения на сопротивлении R от расстройки.

Исходя из операций с комплексными амплитудами, легко получить выражения для напряжений на всех элементах рассматриваемого колебательного контура. Для комплексной амплитуды напряжения на конденсаторе получаем

.

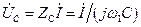Соответственно, фаза напряжения на конденсаторе сдвинута относительно фазы напряжения на резисторе на - p /2. Резонанс напряжения на ёмкости получается при , т. е. при более низкой, чем w ₀ частоте w ₁.

Для комплексной амплитуды напряжения на индуктивности получаем

.

Фаза напряжения на индуктивности сдвинута относительно фазы напряжения на резисторе на p /2. Резонанс напряжения на индуктивности достигается при , т. е. на более высокой, чем w ₀ частоте w ₁. Нужно отметить, что для достаточно высокой добротности контура эта разница частот резонанса напряжений на резисторе, конденсаторе и индуктивности несущественна. Все три максимума совпадают только при Q ₀ ® ¥.