Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Несобственные интегралы от неограниченных функций

Пусть функция y=f(x) непрерывна " х, 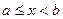и 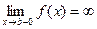, то для любого 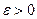функция 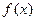интегрируема на сегменте .

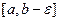Если существует конечный предел 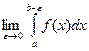, то этот предел называют несобственным интегралом от неограниченной функции f(x) и обозначают символом 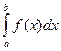. В этом случае говорят, что несобственный интеграл существует или сходится. Если указанный предел не существует, то говорят, что несобственный интеграл не существуе т или расходится.

По определению имеем

= .

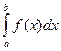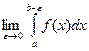Аналогично определяется несобственный интеграл в случае .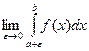

Если f(x) не ограничена при приближении х справа к точке а, то

= .

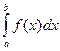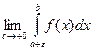Если же функция f(x) не ограничена в некоторой внутренней точке с сегмента [ a, b ] и функция f(x) не ограничена в любой окрестности точки с, то

= + .

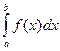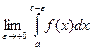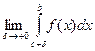Таким образом, из определений непосредственно видно, что несобственный интеграл от неограниченной функции является не пределом интегральных сумм, а пределом определенного интеграла.

Пример. Исследовать на сходимость интеграл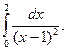

Решение. Подынтегральная функция 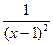не ограничена в точке х = 1. Поэтому рассмотрим отдельно интегралы 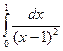и 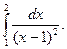Оба интеграла расходятся, так как

.

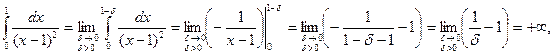
Следовательно, несобственный интеграл 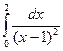расходится.

Практическое занятие 12

1 Вычисление площадей плоских фигур

Вычисление площади плоской фигуры в декартовой системе координат.

Если на сегменте [a, b] непрерывная функция f(x) ³, то площадь криволинейной трапеции, ограниченной кривой y = f(x), осью Oх и прямыми х = а и x = b, равна определенному интегралу

.

В общем случае, если фигура, представляет собой часть плоскости, ограниченной непрерывными кривыми 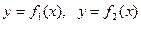, , 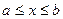() и двумя отрезками прямых x = a, x = b (отрезки прямых могут вырождаться в точку), то площадь такой фигуры можно представить в виде суммы и (или) разности площадей криволинейных трапеций.

у

S

О a b x

Для вычисления площади такой фигуры будем иметь формулу

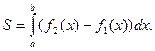
Пример. Найти площадь фигуры, ограниченной линиями: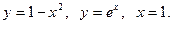

Решение. Сделаем схематический чертеж. Построим данные линии.

у

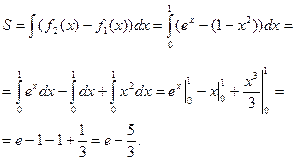1 х

Пусть кривая, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениями 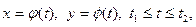причем 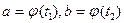. Тогда площадь фигуры D может быть вычислена по формуле

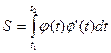
Вычисление площади в полярной системе координат.

Пусть плоская фигура D расположена в полярной системе координат и представляет собой криволинейный сектор, ограниченный непрерывной кривой 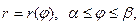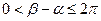и отрезками лучей j = a и j = b. Отрезки лучей могут вырождаться в точку. Тогда площадь фигуры вычисляется по формуле

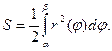
Пример. Найти площадь фигуры, ограниченной кардиоидой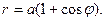

Решение. Область определения функции будет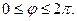
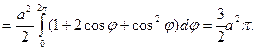