Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Вычисление объемов тел вращения

Объем тела, образованного вращением вокруг оси О х криволинейной трапеции, ограниченной прямыми х = а, х = b, графиком функции y = f(x) и отрезком оси Ох, вычисляется по формуле

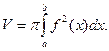
Объем тела, образованного вращение вокруг оси О у криволинейной трапеции, ограниченной прямыми у = с, у = d, графиком функции x = φ (y) и отрезком оси О y, вычисляется по формуле

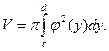
Пример. Эллипс, большая ось которого равна 2 а, малая – 2 b (а > b), вращается: 1) вокруг оси О х; 2) вокруг оси О у. Найти объем получившегося эллипсоида вращения. В частном случае определить объем шара.

Решение. Найдем объем тела, образованного вращением эллипса вокруг оси О х. Напишем уравнение эллипса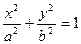

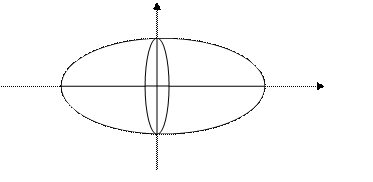
Из уравнения эллипса найдем 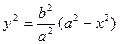. Учитывая, что эллипс пересекается с осью О х в точках х = а и х = - а, найдем объем тела

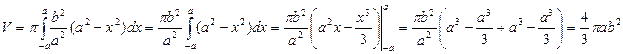
Найдем объем тела, образованного вращением эллипса вокруг оси О у. Аналогично получаем,

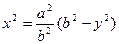и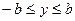

Тогда

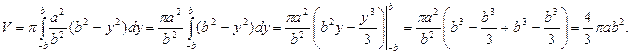Частный случай эллипсоида вращения, когда a = b, есть шар. Таким образом, объем шара 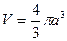, где а – радиус шара.