Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Преобразование кривой регрессии в прямую линию

Если из теоретических соображений или на основе графического анализа можно предположить, что опытные данные описываются степенной функцией типа: 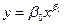; (12.29)

или показательной функцией: 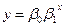; (12.30)

или иной другой, которая может быть преобразована к линей­ному виду относительно переменных, то регрессионный анализ осуществляют по отношению к преобразованным переменным. Выражения преобразуют к линейному виду путем логарифмирования. В результате получают соответственно:

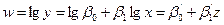; (12.31)

и 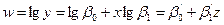; (12.32)

Однако использование метода наименьших квадратов примени­тельно к преобразованным переменным позволяет минимизировать сумму квадратов отклонений w, равную

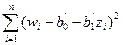; (12.33)

а не исходных значений у.

В случае, когда вид функции, связывающей переменные х и у, точно известен, рекомендуется для получения уточненных оценок параметров в уравнении регрессии делать их оценку с помощью корректированной суммы квадратов отклонений

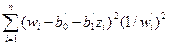; (12.34)

где 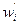- производная функции w по у, взятая в точке у = у_i. Дифференцируя по 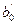и 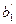и приравнивая обе производные нулю, получим после преобразования

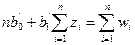; и 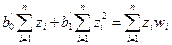; (12.35)

Аналогично имеем

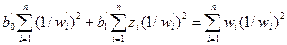и

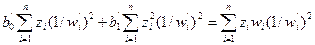; (12.36)

Решая системы уравнений относительно 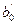и 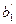, найдем соответствующие оценки.