Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Логарифмически нормальное распределение

Проиллюстрируем проверку гипотезы о логарифмически нор­мальном распределении на материале, что был использован в предыдущем параграфе. Можно предположить, что содержание FеО в шлаке перед раскислением не бывает ниже 9%. В соответствии с этим принимаем y_i = log (x_i - 9).

Таблица 11.1- Результаты расчета значений оценок х x   0, 0175   0, 753   0, 105   0, 823   0, 158   0, 842   0, 263   0, 912   0, 368   0, 930   0, 403   0, 937   0, 543   0, 965   0, 648   0, 983 Таблица 11.2- Значения р и uр р uр р uр р uр 0, 01 —2, 326 0, 30 —0, 524 0, 80 0, 841 0, 02 —2, 054 0, 35 —0, 385 0, 85 1, 036 0, 03 —1, 881 0, 40 —0, 253 0, 90 1, 282 0, 04 —1, 751 0, 45 —0, 126 0, 93 1, 476 0, 05 —1, 645 0, 50 0, 000 0, 95 1, 645 0, 07 —1, 476 0, 55 0, 126 0, 96 1, 751 0, 10 —1, 282 0, 60 0, 253 0, 97 1, 881 0, 15 —1, 036 0, 65 0, 385 0, 98 2, 054 0, 20 —0, 841 0, 70 0, 524 0, 99 2, 326 0, 25 —0, 674 0, 75 0, 674

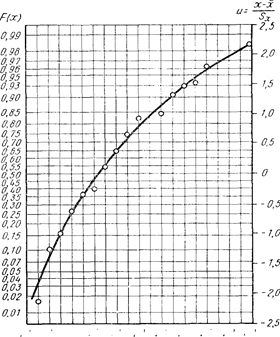Рис. 11.3 Графическая проверка гипотезы о нормальном распределении случайной величины

Построение шкалы для F(х), не отличается от описанного выше. Изменяется только шкала на оси абсцисс, на которой вместо х; наносятся значения y_i = log (x_i - 9). Нанесенные на график оценки хорошо ложатся на прямую. Таким образом, опытные данные не противо­речат сделанному предположению, что содержание FеО в шлаке подчиняется логарифмически нормальному распределению. Перпендикуляр, опущенный на ось абсцисс из точки пересе­чения прямой, проведенной через опытные точки, с горизонталью, отвечающей F(у) = 0, 5, дает оценку среднего значения у. В рас­сматриваемом случае у == 0, 83.

Перпендикуляры, опущенные на ось абсцисс из точек пересе­чения прямой, аппроксимирующей наблюденные значения пере­менной, с прямыми, проведенными параллельно оси абсцисс через точки, соответствующие значениям u = -1 и +1, отсекают на оси абсцисс отрезок, равный двум стандартам. Таким образом, если последнюю величину разделить на 2, то получим оценку среднего квадратического отклонения. В рассматриваемом при­мере эта оценка равна

s = (1, 08 —0, 58)/2 =- 0, 25. (11.16)

Проверка предположения о возможности аппроксимации на­блюденных значений случайной величины с помощью логарифмически нормального распределения по критерию 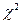, также свидетельствует, что оно допустимо.

Контрольные вопросы:

1. Как осуществляется выбор аппроксимирующего распределения данных.

2. Методы аппроксимации эмпирических распределений, метод выбора и оценки параметров аппроксимирующего распределения Пирсона.

3. Что называют статистическими гипотезами отно­сительно закона распределения рассматриваемой величины, как оценить правильность гипотез.

4. Оценка уровней значимости для отбраковки гипотез.

5. Графический метод проверки правильности гипотез о законе распределения.