Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Нормальное распределение. Из применяемых в статистике распределений наиболее часто пользуются нормальным распределением

Из применяемых в статистике распределений наиболее часто пользуются нормальным распределением. Применение модели обусловлено тем, что согласно централь­ной предельной теореме - распределение среднего n независимых случайных величин, распределенных по любому закону с конеч­ными математическими ожиданиями и дисперсиями, прибли­жается к нормальному, когда число n наблюдений в выборке стремится к бесконечности.

Распределение выборочного среднего стремится к нормальному и при относительно небольших n, если распределения всех независимых случайных величин не сильно отклоняются от нормального и их дисперсии, приблизи­тельно равны друг другу.

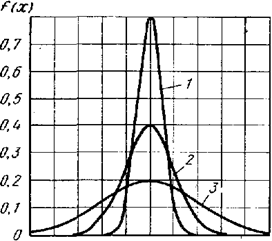
Рис.10.1- Нормальные распределе­ния с одинаковыми v = 0 и раз­личными

значениями 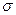: 1 — 0, 5; 2 — 1, 0; 3 — 2, 0

Таким образом, если случайную вели­чину можно рассматривать как результат большого числа неза­висимых равновеликих воздействий, то есть основания считать, что она имеет нормальное или гауссово распределение. Примерами нормально распределенных величин могут служить ошибки измерения, результаты испытания стали на прочность и ударную вязкость, часовая производительность мартеновских печей, масса слитков, отлитых в однотинные изложницы и др. Кроме того, при соблюдении некоторых (в каждом случае своих) условий- нормальным рас­пределением аппроксимируют дру­гие распределения.

Нормальное (гауссово) распределе­ние определяется выра­жениями:

· плотности 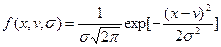(10.1)

· интегральной функции распре­деления

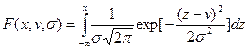(10.2)

в которых 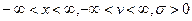и где: v - центр распределения (его математическое ожидание); 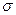- стандартное отклонение, масштабирующее рассеяние.

Основные характеристики, нормального распределения:

· Среднее МХ = v_x

· Дисперсия DХ =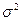

· Третий центральный момент 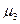=0

· Четвертый центральный момент 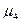= 3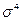

· Коэффициент вариации 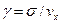у

· Коэффициент асимметрии Sk = 0.

· Коэффициент эксцесса Ех = 3.

Если вместо нормально распределенной случайной величины Х использовать величину отклонения Х от его математического ожидания v_x, отнесенную к стандартному отклонению 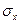, т. е. если ввести случайную величину:

Y= (X -v_x)/ 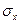, (10.3)

то эта величина будет распределена по нормальному закону при v_y = 0 и 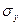= 1. Величину Y называют нормированным откло­нением случайной величины. Для нормированного отклонения, распределенного по нор­мальному закону:

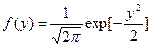(10.4)

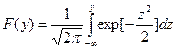(10.5)

где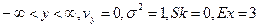

Значения плотности вероятности и интегральной функции распределения, называемого нормированным нормальным распре­делением, табулированы и приведены в учебниках по математической статистике и в специальных математических справочниках. Поскольку нормальное распределение симметрич­ное, в таблицах обычно приводят значения интегральной функ­ции F (у; 0, 1) только для у > = 0. Значения интегральной функции для у < 0 определяются из равенства

F (-у; 0, 1) = 1 - F (у; 0, 1) (10.6)

Значения плотности вероятности f(у) = f (-у), в таблицах их приводят для у > = 0.