Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Схемы из элементарных автоматов

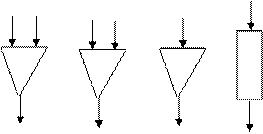Пусть A = { 0, 1 }. Следующие автоматы называются элементарными (см. рис. 7.16):

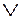& - Z

Рис. 7.16

Здесь первые три автомата представляют собой уже известные функциональные элементы, которые для любых входных наборов вычисляют значения соответствующих булевских функций.

Эти автоматы имеют по одному внутреннему состоянию.

Автомат Z является задержкой для алфавита A = { 0, 1 }.

Рассмотрим как с помощью схем, составленных из элементарных автоматов, можно представлять произвольные автоматы.

Пусть Â = (A, B, Q, j, y) - произвольный автомат, для которого:

A = { a ₁,..., a _m }, B = { b ₁,..., b _n }, Q = { q ₀,..., q _r }, и q ₀ - это начальное состояние автомата Â.

Будем представлять символы алфавитов A и B, а также элементы множества состояний Q с помощью двоичных наборов длины p = ] log ₂(m)[, d = ] log ₂(n)[ и s = ] log ₂(r + 1)[ соответственно.

Заметим, что значения p, d и s выбраны из соображений минимальности длины наборов, которых должно быть не меньше, чем элементов соответствующих множеств.

Для определенности положим, что начальное состояние Â, равное q ₀, представляется набором, состоящим из s нулей.

Рассмотрим автомат Á, имеющий p входов и d выходов, который моделирует работу автомата Â.

Состояния Á представляются двоичными наборами, имеющими длину s, которые соответствуют состояниям Â.

Начальным состоянием автомата Á является состояние, представляющее состояние q ₀ автомата Â.

Если в некоторый момент времени на вход Á поступает набор, представляющий символ входного алфавита a _i и автомат находится в состоянии, соответствующем состоянию q _j, то на выходе Á появляется двоичный набор, представляющий
y(a _i, q _j). При этом сам автомат Á переходит в состояние, представляющее состояние j(a _i, q _j).

Канонические уравнения для автомата Á можно записать в виде:

Здесь (x ₁(t),..., x _p (t)) обозначает набор символов, поступающих на входы Á в момент t, а (q ₁(t),..., q _s(t)) - набор, задающий состояние автомата Á в тот же момент времени.

Функция j _i, i = 1,..., s, определяет значение i -й компоненты состояния автомата Á, в которое он переходит из состояния (q ₁(t),..., q _s(t)) под действием входного символа (x ₁(t),..., x _s(t)).

Функция y _j, j = 1,..., d, определяет значения символа на j -м выходе Á в момент t, для входного символа (x ₁(t),..., x _s(t)) и текущего состояния (q ₁(t),..., q _s(t)).

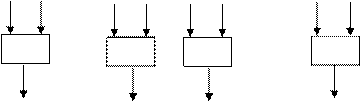
Поскольку функции j _i, i = 1,..., s, и y _j, j = 1,..., d являются булевскими функциями, то они могут быть реализованы схемами из функциональных элементов, которые изображены на рис. 7.17.

........

y₁ ... y _d j₁ ... j_s

Рис. 7.17

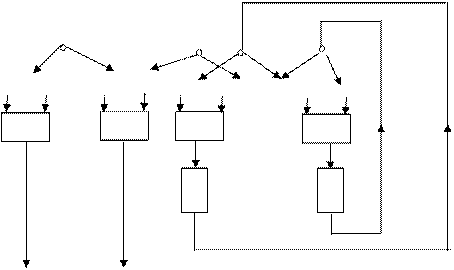
Рассмотрим автоматную схему, представляющую автомат Á, которая изображена на рис. 7.18:

x ₁... x _p q ₁ ... q _s