
Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Упражнение. 1. Показать, что автоматы Á1 и Á2 эквивалентны тогда и только тогда, когда множества функций
|
|
1. Показать, что автоматы Á 1 и Á 2 эквивалентны тогда и только тогда, когда множества функций, вычисляемых этими автоматами из различных состояний как начальных, совпадают.
2. Показать, что всякий автомат эквивалентен самому себе.
ОПРЕДЕЛЕНИЕ
Автомат, все состояния которого являются отличимыми, называется минимальным автоматом.
Пусть Á = (A, B, Q, j, y) - некоторый автомат.
Обозначим как j* функцию j*: A * 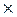 Q
Q 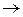 Q, которая для любого входного слова
Q, которая для любого входного слова  и состояния q i принимает значение, равное состоянию Á после переработки
и состояния q i принимает значение, равное состоянию Á после переработки  из начального состояния q i.
из начального состояния q i.
Эта функция может быть определена следующими соотношениями:
1) " a Î A (j*(a, q i) = j(a, q i));
2) "  Î A *, a Î A (j* (
Î A *, a Î A (j* ( a, q i) = j(a, j*(
a, q i) = j(a, j*( , q i))).
, q i))).
Замечание. Функцию j* можно использовать для определения функций, вычисляемых автоматами.
Функция 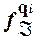 может быть задана соотношениями:
может быть задана соотношениями:
1) " a Î A (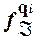 (a) = y(a, q i));
(a) = y(a, q i));
2) "  Î A *, a Î A (
Î A *, a Î A (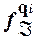 (
( a)=
a)= 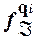 (
( ) y(a, j*(
) y(a, j*( , q i)).
, q i)).
|
|
