Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Доказательство. Рассмотрим последовательность отношений k–неотличимости состояний автомата Á: r1,
|
|
Рассмотрим последовательность отношений
k –неотличимости состояний автомата Á: r 1,..., r k,...
Поскольку Á имеет отличимые состояния, то r1 разбивает множество состояний Á не менее чем на два класса
1- неотличимых состояний. (В противном случае все состояния Á являются неотличимыми, поскольку 1 – неотличимость всех сотояний автомата означает, что значения функции выхода зависят только от входных символов.)
Согласно лемме 3, если r i É ri+1, то число классов (i + 1)-неотличимых состояний автомата хотя бы на 1 больше числа классов i -неотличимых состояний.
Поскольку автомат имеет n состояний, то найдется такое значение i < n, что справедлива цепочка включений:
r1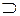 
... r i - 1 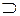r i = r i +1 ...
Справедливость последнего свойства следует из того, что каждый элемент разбиения множества состояний Á на множества i -неотличимых состояний должен содержать хотя бы одно состояние.
Следовательно, r i = e.
Поэтому, если состояния q i и q j являются отличимыми, то они должны различаться хотя бы на одном слове, длина которого не превосходит n - 1.
|
|