Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
Определение
|
|
Операцией обратной связи называется преобразование конечного автомата Â, при котором один из выходов Â подключается к входу автомата Z, а выход Z подсоединяется к одному из входов Â.
В результате операции обратной связи образуется новый автомат с m - 1 входами и n - 1 выходами.
Пример. На рис. 7.14 изображен конечный автомат Á, который получается из автомата Â, имеющего по два входа и выхода, применением обратной связи:
 |
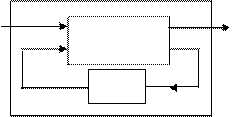x (t) y (t)
Â
Z
Á
Рис. 7.14
Состояниями Á являются пары (q i, q j), где q i - состояние Â, а q j - состояние автомата задержки Z.
Пусть q 0- начальное состояние автомата Á.
Тогда функционирование автомата Â для заданных начальных состояний q 0 и a 0 представляется следующими каноническими уравнениями:
| q1(t0) | = | q0; |
| q2(t0) | = | a0; |
| q1(t+1) | = | j((x (t), q2(t)), q1(t)); |
| q2(t+1) | = | y2((x (t), q2(t)), q1(t)); |
| y(t) | = | y1((x (t), q2(t)), q1(t)). |
Здесь q 1(t) и q 2(t) - состояния Â и Z в момент t, а y1 и y2 - функции, определяющие символы на первом и втором выходах автомата Â соответственно.
Входные символы для автомата Â представляют собой пары символов (x 1(t), x 2(t)).
Упражнение. Записать канонические уравнения для автомата задержки на два шага, изображенного на рис. 7.15.
 |
Z Z
Рис. 7.15
|
|