Главная страница Случайная страница
Разделы сайта
АвтомобилиАстрономияБиологияГеографияДом и садДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеталлургияМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРелигияРиторикаСоциологияСпортСтроительствоТехнологияТуризмФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Для новых пользователей первый месяц бесплатно. Чат-бот для мастеров и специалистов, который упрощает ведение записей: — Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать; Начать пользоваться сервисом
ОПРЕДЕЛЕНИЕ. Состояния qi и qj автомата Áназываются отличимыми, если существует такое входное слово , что
|
|
Состояния q i и q j автомата Á называются отличимыми, если существует такое входное слово 
, что
() 
().
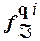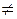
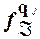Отличимость двух состояний q i и q j означает, что существует входное слово , которое из этих состояний как начальных перерабатывается в разные выходные слова.
В качестве примера рассмотрим автомат, изображенный на рис. 7.6.
0 (0) 0 (0)
q0 q 1
0 (1) 1 (1) 1 (1)
1 (0) q2
Рис. 7.6
Состояния q 0 и q 1 заданного автомата неотличимые. Это так поскольку первый символ произвольного входного слова из состояний q 0 и q 1 как начальных перерабатывается одинаково. При этом автоматв обоих случаях переходит в одно и то же состояние. Поэтому дальнейшая переработка слова из начальных состояний q 0и q 1 продолжается одинаково.
Состояния q 0 и q 2 рассматриваемого автомата являются отличимыми так как, например,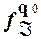 
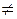
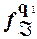(0) 
(0).
Если состояния q i и q j автомата - являются отличимыми, то функци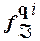и 
() и 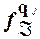() различаются на бесконечном множестве слов.
Действительно, если для некоторого имеет место соотношение 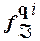() ¹ 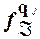(), то для любого слова 
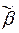также справедливо 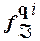( 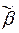) |¹ ( ).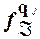
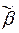Функции, вычисляемые автоматами, имеют бесконечные области определения. Поэтому невозможна конструктивная проверка отличимости состояний на основе только определения отличимости.
С целью отыскания метода для распознавания отличимых состояний произвольных автоматов рассмотрим вопрос о длине кратчайшего слова, которое по-разному перерабатывается из двух отличимых состояний q i и q j. Прежде всего отметим, что длина кратчайшего слова может быть сколь угодно большой.
Пусть Á - это автомат с n состояниями, диаграмма переходов которого приведена на рис. 7.7.
0 (0) 0 (0) 0 (0)
0 (0) 
q1q 2 .... q n
1 (1) 1 (1) 1 (1)
1 (0)
— Регулярная проверка качества ссылок по более чем 100 показателям и ежедневный пересчет показателей качества проекта.
— Все известные форматы ссылок: арендные ссылки, вечные ссылки, публикации (упоминания, мнения, отзывы, статьи, пресс-релизы).
— SeoHammer покажет, где рост или падение, а также запросы, на которые нужно обратить внимание.
SeoHammer еще предоставляет технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Зарегистрироваться и Начать продвижение
Рис 7.7
Состояния q 1 и q 2 этого автомата являются отличимыми, и длина кратчайшего слова, на котором они различаются, равна n - 1.
Действительно, для любого входного слова первые n - 1 символов этого слова одинаково перерабатываются автоматом из состояний q 1 и q 2. После этого Á переходит в состояние q n, если он начал работу из состояния q 2, и в состояние q n- 1, если Á начинает работу из состояния q 1. Из q n- 1 и q n как начальных состояний всякое односимвольное слово перерабатывается по-разному. Поэтому n -й символ любого входного слова перерабатывается из состояний q 0и q 1 в разные выходные слова.
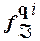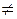
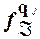Покажем, что если состояния q i и q j автомата Á, имеющего n состояний, отличимые, и - это кратчайшее слово, для которого () (), то | | 
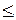n - 1.
|
|