Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

ОПРЕДЕЛЕНИЕ. Числовая функция f: Nk ® N вычисляется конечным автоматом Â из состояния qr, если:

Числовая функция f: N^k ® N вычисляется конечным автоматом Â из состояния q_r, если:

" n ₁,..., n _k Î N (f (n ₁,..., n _k) = m Û = ).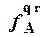

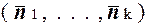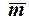Для числовых функций, вычисляемых автоматами, будем использовать те же обозначения, что и для словарных функций: .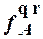

Пример. На рис. 7.3 изображена диаграмма переходов автомата, который из начального состояния q ₀ вычисляет функцию f (x) = 2 x.

1 (0)

0 (0) q ₀ q ₁ 1 (1)

0 (1)

Рис. 7.3

При этом достаточно достаточно потребовать, чтобы входное слово, представляющее произвольное число, всегда имело один незначащий нуль.

Последнее предположение требуется для того, чтобы длина результата равнялась длине входного слова.

Состояния q ₀ и q ₁ приведенного автомата необходимы для запоминания значения переноса в старший разряд при поразрядном умножении входного числа на 2.

На диаграммах автоматов наборы значений одноименных разрядов чисел n ₁,..., n _k будем представлять горизонтальными последовательностями.

Пример. На рис. 7.4 изображена диаграмма переходов автомата, который из начального состояния q ₀ вычисляет функцию f (x, y) = 2x + y.

Входным алфавитом этого автоматаявляется множество: { 00, 01, 10, 11 }.

01 (1) 10 (0) 01 (0)

q ₀ q₁ 10 (1)

00 (0) 00 (1)

11 (1)

11 (0) 00 (0)

q ₂ 01 (1)

10 (0), 11 (1) Рис. 7.4

Состояния q ₀, q ₁ и q ₂ приведенного автомата соответствуют запоминанию значений переноса в старшие разряды значений 0, 1 и 10. В последнем случае имеет место перенос в два последующих разряда входных чисел: в первый из последующих разрядов ничего не добавляется, а во второй добавляется 1.