Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

ОПРЕДЕЛЕНИЕ. Словарная функция f: A* B* вычисляется автоматом Â = (A, B, Q, j, y) из начального состояния qr

Словарная функция f: A 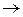^* B ^* вычисляется автоматом Â = (A, B, Q, j, y) из начального состояния q_r, если для любого слова 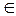A ^* выполняется соотношение:

" Î A ^* (f () = 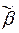Û Â из начального состояния q_r перерабатывает в ).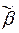

Для функции, которая вычисляется автоматом Â из состояния q_r, применяется обозначение .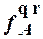

Пример. Рассмотрим словарную функцию f: A ^* ® B ^*, где A = { a, b }, B = { a, b }, которая заменяет в произвольном входном слове 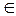A ^* каждое третье вхождение символа b на символ a, а все остальные символы входного слова функция оставляет без изменения.

Диаграмма переходов автомата, который из начального состояния q ₀ вычисляет эту функцию, приведена на рис. 7.2.

b (b)

q ₀ q ₁

a (a) a (a)

b (a) b (b)

a (a) q ₂

Рис. 7.2

Уточним понятие функций, вычисляемых конечными автоматами, для числовых функций.

Пусть входным и выходным алфавитами автомата является множество { 0, 1 }. Тогда входные и выходные слова этого автомата можно интерпретировать как двоичные записи целых неотрицательных чисел в двоичной системе. Возможно, что такие записи имеют незначащие нули.

Для конечных автоматов естественно подавать на вход записи чисел в двоичной системе справа налево, поскольку многие традиционные схемы арифметических вычислений предполагают обработку цифр записей чисел, начиная с младших разрядов записей чисел.

Поскольку входные слова конечных автоматов, в том числе и такие, которые представляют числа, по определению поступают на вход автоматов в противоположном порядке, то будем представлять числа, подаваемые на входы автоматов в виде слов, являющихся инвертированными записями таких чисел.

Пусть n - произвольное целое неотрицательное число. Обозначим как 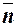- всякую инвертированную двоичную запись этого числа, в которой допускается существование незначащих нулей.

Незначащие нули приходится использовать из-за того, что реальные арифметические функции могут отображать числа одной длины в числа, записи которых имеют другую длину (большую или меньшую). Поскольку длины входных слов и выходных слов автоматов всегда совпадают, то в дальнейшем двоичные числа всегда будут представляться с точности до необходимого числа незначащих нулей в них, что позволяет вычислять числовые функции с помощью автоматов и тогда, когда длина записи числа результата больше длины числа, исходного данного.

Если числовая функция f отображает N^k в N, то всякий набор чисел, принадлежащий области определения этой функции, будем представлять словом, символами которого являются последовательности значений одноименных разрядов чисел этого набора.

Пусть n ₁,..., n _k это числа из N, представленные записями равной длины, получаемыми добавлением произвольного количества незначащих нулей.

Запись 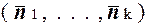обозначает слово в алфавите
{ 0, 1 } ^k, первый символ которого представляет значения самого младшего разряда всех чисел n ₁,..., n _k, второй - значения следующего разряда этих чисел и так далее. Заметим, что { 0, 1 } ^k это все k -символьные последовательности из нулей и единиц.