Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Задача. Определить главные напряжения в опасной точке стержня, подвергающегося совместному действию изгиба и кручения:

Определить главные напряжения в опасной точке стержня, подвергающегося совместному действию изгиба и кручения:

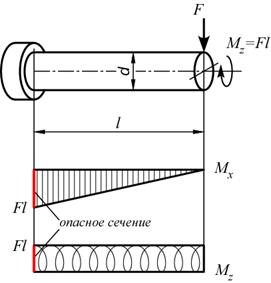
Построив эпюры внутренних силовых факторов, заключаем, что опасным сечением стержня является сечение заделки, в котором действует наибольший по величине изгибающий момент M_x.

Для нахождения опасной точки в опасном сечении рассмотрим распределение нормальных и касательных напряжений по опасному сечению:

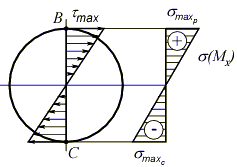
В данном случае имеется две равноопасные точки – B и C, в которых действуют максимальные нормальные и касательные напряжения, одинаковые по величине, но разные по направлению. Рассмотрим напряженное состояние в точке В, выделив в её окрестности элементарный объем и расставив вектора напряжени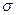й и 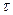на его гранях.

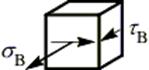
Величины напряжени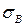й и 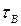можно определить по формулам:

,

.

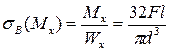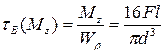Рассмотрим выделенный куб со стороны грани, свободной от напряжений (сверху):

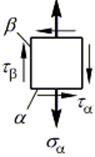
Обозначим две взаимно перпендикулярные площадки a и b. На площадке a действуют нормальное 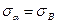и касательное напряжение 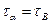. На площадке b действуют только касательное напряжение 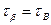(согласно закону парности касательных напряжений).

Порядок построения круга Мора:

1. В системе координат t-s нанести точки с координатами 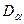(s_a , t_a) и 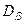(s_b , t_b). При этом нормальное напряжение считается положительным, если оно вызывает растяжение, а касательное – если оно действует по часовой стрелке относительно центра элемента.

2. Соединить полученные точки D_a и D_b отрезком. Точка пересечения этого отрезка с осью абсцисс O является центром круга Мора.

3. Построить окружность с центром в точке O и радиусом OD_a. Координаты точек пересечения окружности с осью абсцисс дают величины главных напряжений (в нашем случае s ₁, и s ₃).

4. Пересечение площадок a (горизонталь) и b (вертикаль) дает положение полюса площадок круга Мора P _пл (точка, в которой пересекаются все площадки).

5. Провести из полюса P _пл лучи через точки (s ₁, 0) и (s ₃, 0). Эти лучи задают положение главных площадок.

Наносим положение главных площадок и направление главных напряжений на рассматриваемую площадку:

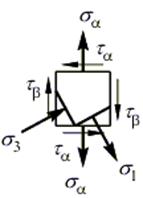
Радиус круга Мора

,

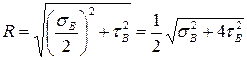тогда главные напряжения

,

.
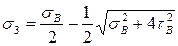