Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Задача. В стержне с площадью поперечного сечения A=5х104 м2, растягиваемом силой F = 50 кН, определить нормальное и касательное напряжения

В стержне с площадью поперечного сечения A= 5х10⁴ м², растягиваемом силой F = 50 кН, определить нормальное и касательное напряжения, возникающие на площадке, наклоненной под углом 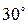к поперечному сечению стержня:

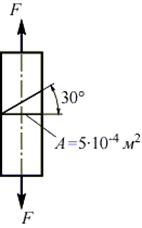
В точках поперечного сечения возникают только нормальные напряжения, то есть площадка элементарного объема в окрестностях точки, совпадающая с этим сечением, является главной:

,

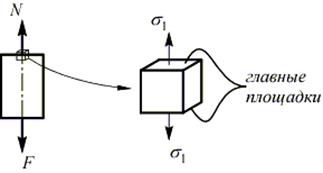
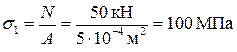остальные главные напряжения отсутствуют, т.е. это одноосное напряженное состояние.

Найдем напряжения на наклонной площадке.

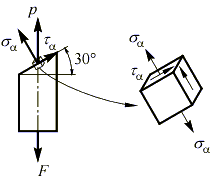
Вектор полного напряжения p, действующий на этой площадке, можно разложить на две составляющие: нормальную s_a и касательную t_a, для определения величины которых воспользуемся кругом Мора.

Наносим в координатах t-s точки, соответствующие главным напряжениям 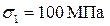и 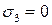, и на этих точках, как на диаметре, строим круг Мора:

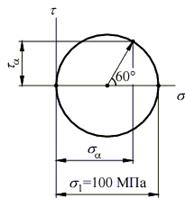
Откладывая от оси абсцисс против часовой стрелки двойной угол a, получаем на круге точку, отображающую состояние на наклонной площадке. Координаты этой точки являются искомыми напряжениями и вычисляются по формулам (2.4) и (2.5):

, .

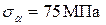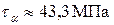Обратная задача Мора

Обратная задача Мора состоит в определении главных напряжений по известным напряжениям на произвольной площадке. Рассмотрим её на конкретном примере.