Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Главные оси и главные напряжения

Рассмотрим множество секущих площадок, проходящих через рассматриваемую точку. По нормали к каждой площадке отложим вектор r с координатами: x = rl, y = rm, z = rn.

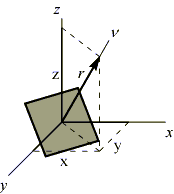
Выразим направляющие косинусы через координаты и длину вектора:

l = x/r, m = y/r, n = z/r.

Подставляя эти выражения в полученную ранее формулу для напряжения на произвольной площадке, получим:

,

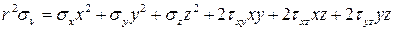откуда длина вектора r

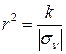, где k – масштабный коэффициент, равный

.

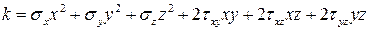Полученное выражение является уравнением центральной поверхности второго порядка, центр которой совпадает с центром координат. При определенном положении системы координат уравнение преобразуется к виду, в котором попарные произведения xy, xz, yz исчезают. Это говорит о том, что в каждой точке нагруженного тела существует такая система координат, в которой касательные напряжения на взаимно перпендикулярных координатных площадках равны нулю. Оси такой системы координат называются главными осями, координатные площадки – главными площадками, а соответствующие им нормальные напряжения – главными напряжениями.

Главные напряжения принято нумеровать в порядке убывания, то есть .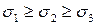

Классификация напряженных состояний в точке

По количеству главных напряжений, возникающих в точке, все напряженные состояния можно разделить на три группы:

1. Одноосное (линейное) напряженное состояние:

(два главных напряжения равны нулю)

2. Плоское напряженное состояние:

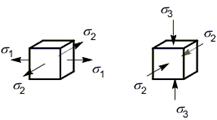
(одно главное напряжение равно нулю)

3. Объемное напряженное состояние:

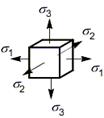
(ни одно из главных напряжений не равно нулю).

Наиболее распространенными в технике являются линейное и плоское напряженные состояния.

Эллипсоид напряжений

Для случая, когда отсутствуют касательные напряжения, компоненты вектора напряжений на произвольной площадке можно выразить следующим образом:

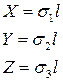
откуда направляющие косинусы

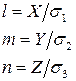
Так как 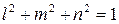, можно записать:

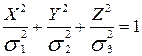
Полученное уравнение является уравнением эллипсоида. Таким образом, геометрическое место концов вектора полного напряжения представляет собой эллипсоид, полуосями которого являются главные напряжения s ₁, s ₂, s ₃:

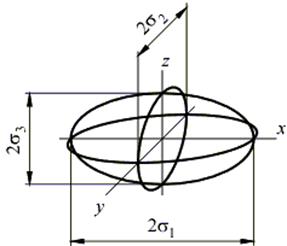
Этот эллипсоид называется эллипсоидом напряжений и представляет собой геометрическую интерпретацию напряженного состояния в точке.