Сервис онлайн-записи на собственном Telegram-боте

Тот, кто работает в сфере услуг, знает — без ведения записи клиентов никуда. Мало того, что нужно видеть свое расписание, но и напоминать клиентам о визитах тоже. Нашли самый бюджетный и оптимальный вариант: сервис VisitTime.
Для новых пользователей первый месяц бесплатно.

Чат-бот для мастеров и специалистов, который упрощает ведение записей:

— Сам записывает клиентов и напоминает им о визите;
— Персонализирует скидки, чаевые, кэшбэк и предоплаты;
— Увеличивает доходимость и помогает больше зарабатывать;

Начать пользоваться сервисом

Как продвинуть сайт на первые места?

Вы создали или только планируете создать свой сайт, но не знаете, как продвигать? Продвижение сайта – это не просто процесс, а целый комплекс мероприятий, направленных на увеличение его посещаемости и повышение его позиций в поисковых системах.

Ускорение продвижения

Если вам трудно попасть на первые места в поиске самостоятельно, попробуйте технологию Буст, она ускоряет продвижение в десятки раз, а первые результаты появляются уже в течение первых 7 дней. Если ни один запрос у вас не продвинется в Топ10 за месяц, то в SeoHammer за бустер вернут деньги.

Начать продвижение сайта

Универсальная теория Мора

Пятая теория прочности – теория предельных состояний (теория Мора).

Критерий равнопрочности: напряженные состояния равнопрочны по наступлению предельного состояния, если при одновременном пропорциональном увеличении главных напряжений их круги Мора одновременно коснутся предельной огибающей.

Если изобразить в координатах t-s семейство кругов Мора для различных предельных состояний материала, то огибающая этого семейства будет предельной огибающей для данного материала.

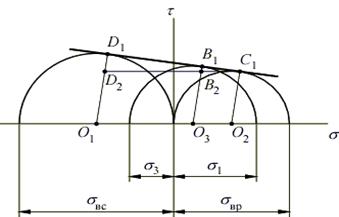
Изобразим в координатах t-s три предельных круга Мора:

- круг с центром в точке O ₁ – для случая одноосного сжатия (главные напряжения σ ₁ = 0, σ ₂ = 0, σ ₃ = σ _вс);

- круг с центром в точке O ₂ – для случая одноосного растяжения (главные напряжения σ ₁ = σ _вр, σ ₂ = 0, σ ₃ = 0);

- круг с центром в точке O ₃ – для случая плоского напряженного состояния (главные напряжения σ ₁, σ ₃).

Линия C ₁ D ₁, огибающая круги, называется предельной огибающей.

Как видно из рисунка, 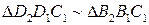, то есть

.

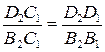Запишем длины отрезков через соответствующие напряжения:

,

,

,

.

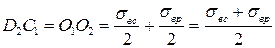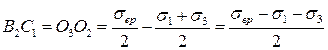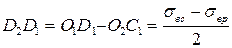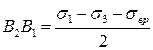Подставляя эти значения в пропорцию, получим

,

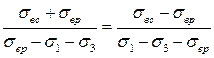откуда:

.

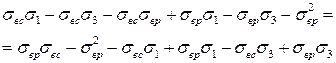После сокращения имеем

,

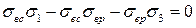тогда

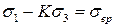, где .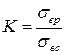

Т.к. 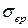– предел прочности для одноосного растяжения, его можно заменить .

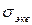Таким образом, эквивалентное напряжение по теории Мора, равно:

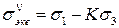. (2.11)

Для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию, 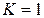, следовательно

,

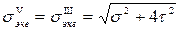то есть теория Мора совпадает с теорией максимальных касательных напряжений.

Для хрупких материалов 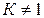, и

.

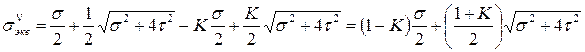Интересно, что для весьма хрупких материалов с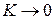

,

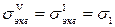то есть теория Мора совпадает с теорией максимальных нормальных напряжений.

Теорию Мора рекомендуется использовать для хрупких (в том числе анизотропных) материалов вместо первой и второй теорий. Ее недостатком является неучет промежуточного главного напряжения σ ₂.